Пусть функция 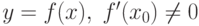 обратима в окрестности точки
обратима в окрестности точки  и
и 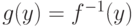 - обратная функция. Тогда производная
- обратная функция. Тогда производная 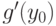 в точке
в точке 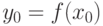 равна
равна
(Отметьте один правильный вариант ответа.)
Варианты ответа
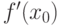

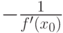
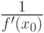 (Верный ответ)
(Верный ответ)

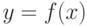 дифференцируема в точке
дифференцируема в точке  и
и 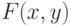 непрерывна в окрестности точки
непрерывна в окрестности точки 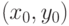 и
и 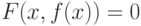 . Пусть существует единственная неявная функция
. Пусть существует единственная неявная функция 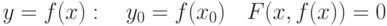 . Тогда
. Тогда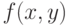 при условии
при условии 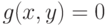 . Тогда линия уровня
. Тогда линия уровня  пересекает кривую
пересекает кривую  под углом
под углом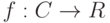 при условии
при условии 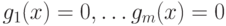 . Пусть задана функция Лагранжа
. Пусть задана функция Лагранжа 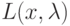 . Тогда особая точка
. Тогда особая точка 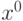 будет точкой условного локального максимума, если для любого допустимого сдвига
будет точкой условного локального максимума, если для любого допустимого сдвига для
для  раз дифференцируемой в окрестности точки
раз дифференцируемой в окрестности точки 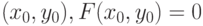 и
и 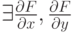 непрерывные в окрестности
непрерывные в окрестности  - множество сходимости последовательности
- множество сходимости последовательности  . Функция
. Функция  является пределом последовательности
является пределом последовательности 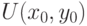 и
и 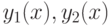 - решения задачи Коши
- решения задачи Коши 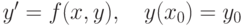 , то
, то