Математическая логика - ответы
Как выглядит на языке кванторов утверждение: "Говорят, что предел последовательности с общим членом 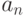 равен
равен  , если для любого сколь угодно большого положительного числа (
, если для любого сколь угодно большого положительного числа (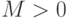 ) найдётся такой натуральный номер
) найдётся такой натуральный номер  , что все элементы последовательности с номерами, начиная с
, что все элементы последовательности с номерами, начиная с  , больше
, больше 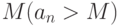 "
"
Как выглядит на языке кванторов утверждение: "Для любого сколь угодно малого положительного числа  существует натуральное число
существует натуральное число  , такое, что, начиная с номера
, такое, что, начиная с номера 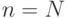 все элементы последовательности отличаются от
все элементы последовательности отличаются от  меньше чем на
меньше чем на  ."
."
Даны значения логических переменных  и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
 |  |  |  |  |  |  |  |  |  |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
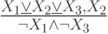
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 1 | 0 | 0 |
Проведите сложение двух пятизначных двоичных слагаемых:  .
.
В ответе приведите значение суммы в двоичной форме, ограничившись пятью младшими разрядами.
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:
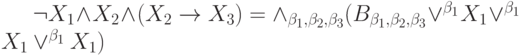
где
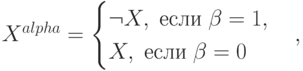
 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
| 1 | 1 | 1 |
Пусть латинские буквы обозначают высказывания:
A - общеутвердительное;
E - общеотрицательное;
O - частноотрицательное;
I - частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | O | 4 |
Проверьте справедливость утверждающе отрицающего модуса
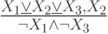
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 0 | 0 | 0 |
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 1 | 0 | 0 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 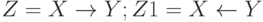 . Каково логическое значение выражения:
. Каково логическое значение выражения:  и
и  .
.
 |  |
|---|---|
| 0 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
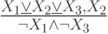
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 1 | 1 | 0 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 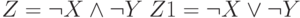 . Каково логическое значение выражения:
. Каково логическое значение выражения:  .
.
 |  |
|---|---|
| 0 | 0 |
Проверьте справедливость утверждающе отрицающего модуса 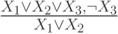
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 1 | 0 | 0 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 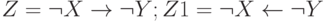 . Каково логическое значение выражения:
. Каково логическое значение выражения:  и
и  .
.
 |  |
|---|---|
| 1 | 0 |
Проведите сложение двух пятизначных двоичных слагаемых:  .
.
В ответе приведите значение второго слагаемого в десятичной форме.
Проведите сложение двух пятизначных двоичных слагаемых:  .
.
В ответе приведите значение суммы в десятичной форме.
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 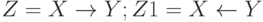 . Каково логическое значение выражения:
. Каково логическое значение выражения:  и
и  .
.
 |  |
|---|---|
| 0 | 1 |
Даны значения логических переменных  и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
 |  |  |  |  |  |  |  |  |  |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
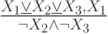
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 0 | 0 | 1 |
Проверьте справедливость утверждающе отрицающего модуса
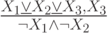
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 1 | 0 | 1 |
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
Все кошки хищники. Собака хищник. Следовательно, собака кошка.
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0:Первый и последний президент СССР - М.С. Горбачёв. Москва - столица СССР. Следовательно, М.С. Горбачёв проживает в Москве.
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
Золото дороже серебра.
Оцените истинность или ложность высказывания:2+2=4 или 2 * 2=5.
Если высказывание истинно, то введите ответ 1, если ложно, то введите 0.
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
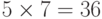 или 13 простое число.
или 13 простое число.
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
225 - это значение квадрата числа 15.
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
Байт - это 8 бит.
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
Если о высказывании нельзя однозначно сказать истинно оно или ложно, то это не высказывание.
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 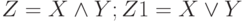 . Каково логическое значение выражения:
. Каково логическое значение выражения:  .
.
 |  |
|---|---|
| 1 | 1 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 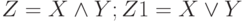 . Каково логическое значение выражения:
. Каково логическое значение выражения:  .
.
 |  |
|---|---|
| 1 | 0 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 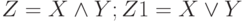 . Каково логическое значение выражения:
. Каково логическое значение выражения:  .
.
 |  |
|---|---|
| 0 | 1 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 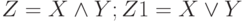 . Каково логическое значение выражения:
. Каково логическое значение выражения:  .
.
 |  |
|---|---|
| 0 | 0 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 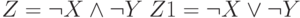 . Каково логическое значение выражения:
. Каково логическое значение выражения:  .
.
 |  |
|---|---|
| 1 | 1 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 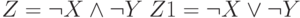 . Каково логическое значение выражения:
. Каково логическое значение выражения:  .
.
 |  |
|---|---|
| 1 | 0 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 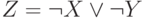 ;
;  . Каково логическое значение выражения:
. Каково логическое значение выражения:  .
.
 |  |
|---|---|
| 0 | 1 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 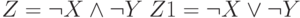 . Каково логическое значение выражения:
. Каково логическое значение выражения:  .
.
 |  |
|---|---|
| 0 | 0 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 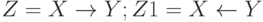 . Каково логическое значение выражения:
. Каково логическое значение выражения:  и
и  .
.
 |  |
|---|---|
| 1 | 0 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 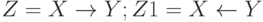 . Каково логическое значение выражения:
. Каково логическое значение выражения:  и
и  .
.
 |  |
|---|---|
| 1 | 1 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 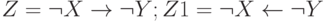 . Каково логическое значение выражения:
. Каково логическое значение выражения:  и
и  .
.
 |  |
|---|---|
| 0 | 0 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 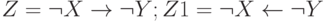 . Каково логическое значение выражения:
. Каково логическое значение выражения:  и
и  .
.
 |  |
|---|---|
| 0 | 1 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 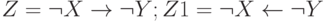 . Каково логическое значение выражения:
. Каково логическое значение выражения:  и
и  .
.
 |  |
|---|---|
| 1 | 1 |
Представьте формулу алгебры высказываний в дизъюнктивной нормальной форме:
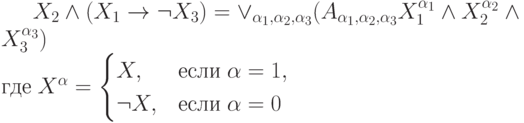
 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 0 | 0 | 0 |
Представьте формулу алгебры высказываний в дизъюнктивной нормальной форме:
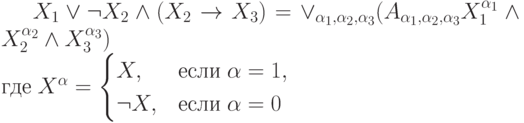
 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 0 | 0 | 1 |
Представьте формулу алгебры высказываний в дизъюнктивной нормальной форме:
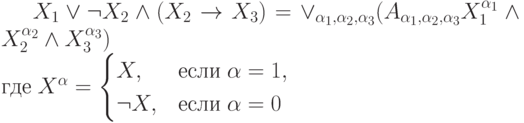
 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 0 | 1 | 0 |
Представьте формулу алгебры высказываний в дизъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 0 | 1 | 1 |
Представьте формулу алгебры высказываний в дизъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 1 | 0 | 0 |
Представьте формулу алгебры высказываний в дизъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 1 | 0 | 1 |
Представьте формулу алгебры высказываний в дизъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 1 | 1 | 0 |
Представьте формулу алгебры высказываний в дизъюнктивной нормальной форме:
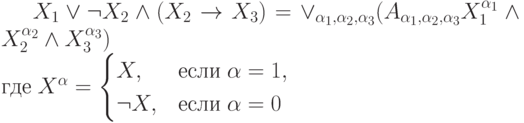
 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 1 | 1 | 1 |
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:
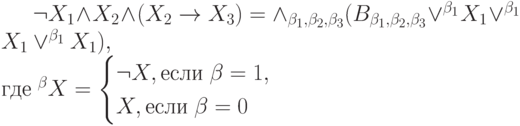
 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 0 | 0 | 0 |
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 0 | 0 | 1 |
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:
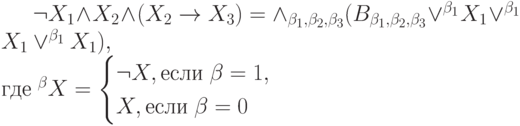
 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 0 | 1 | 0 |
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 0 | 1 | 1 |
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:
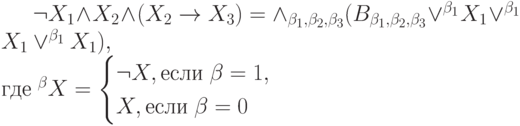
 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 1 | 0 | 0 |
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 1 | 0 | 1 |
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 1 | 0 | 0 |
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 1 | 1 | 1 |
Даны значения логических переменных  и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
 |  |  |  |  |  |  |  |  |  |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 |
Даны значения логических переменных  и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
 |  |  |  |  |  |  |  |  |  |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
Даны значения логических переменных  и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
 |  |  |  |  |  |  |  |  |  |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
Даны значения логических переменных  и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
 |  |  |  |  |  |  |  |  |  |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
Даны значения логических переменных  и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
 |  |  |  |  |  |  |  |  |  |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
Даны значения логических переменных  и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
 |  |  |  |  |  |  |  |  |  |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
Даны значения логических переменных  и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
 |  |  |  |  |  |  |  |  |  |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
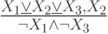
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 0 | 0 | 1 |
Проверьте справедливость утверждающе отрицающего модуса
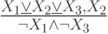
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 0 | 1 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
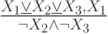
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 0 | 1 | 1 |
Проверьте справедливость утверждающе отрицающего модуса
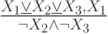
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 1 | 0 | 1 |
Проверьте справедливость утверждающе отрицающего модуса
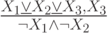
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 1 | 1 | 1 |
Проверьте справедливость утверждающе отрицающего модуса 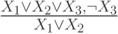
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 0 | 0 | 0 |
Проверьте справедливость утверждающе отрицающего модуса 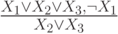
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 0 | 0 | 1 |
Проверьте справедливость утверждающе отрицающего модуса 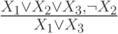
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 0 | 1 | 0 |
Проверьте справедливость утверждающе отрицающего модуса 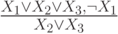
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 0 | 1 | 1 |
Проверьте справедливость утверждающе отрицающего модуса 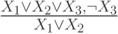
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 1 | 0 | 1 |
Проверьте справедливость утверждающе отрицающего модуса 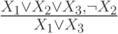
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 1 | 1 | 0 |
Проведите сложение двух пятизначных двоичных слагаемых:  .
.
В ответе приведите значение первого слагаемого в десятичной форме.
Проведите сложение двух пятизначных двоичных слагаемых:  .
.
В ответе приведите значение второго слагаемого в десятичной форме.
Проведите сложение двух пятизначных двоичных слагаемых:  .
.
В ответе приведите значение суммы в двоичной форме.
Проведите сложение двух пятизначных двоичных слагаемых:  .
.
В ответе приведите значение суммы в двоичной форме, ограничившись пятью младшими разрядами.
Проведите сложение двух пятизначных двоичных слагаемых:  ; ограничившись пятью младшими разрядами. В ответе приведите значение в десятичной форме.
; ограничившись пятью младшими разрядами. В ответе приведите значение в десятичной форме.
Заданы три функции:
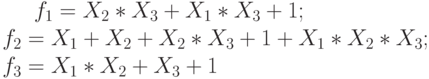
Функция 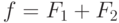 .
.
Проверьте, является ли она сохраняющей ноль.
Если да, то 1, если нет - 0.
Заданы три функции:
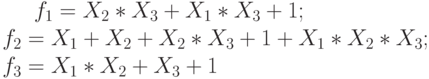
Функция 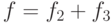 .
.
Проверьте, является ли она сохраняющей единицу.
Если да, то 1, если нет то 0.
Заданы три функции:
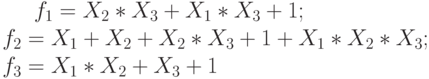
Функция 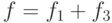 .
.
Проверьте, является ли она самодвойственной.
Если да, то 1, если нет то 0.
Пусть латинские буквы обозначают высказывания:
A - общеутвердительное;
E - общеотрицательное;
O - частноотрицательное;
I - частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | A | 1 |
Пусть латинские буквы обозначают высказывания:
A - общеутвердительное;
E - общеотрицательное;
O - частноотрицательное;
I - частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | O | 1 |
Пусть латинские буквы обозначают высказывания:
A - общеутвердительное;
E - общеотрицательное;
O - частноотрицательное;
I - частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | I | 2 |
Пусть латинские буквы обозначают высказывания:
A - общеутвердительное;
E - общеотрицательное;
O - частноотрицательное;
I - частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| E | A | 2 |
Пусть латинские буквы обозначают высказывания:
A - общеутвердительное;
E - общеотрицательное;
O - частноотрицательное;
I - частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | E | 3 |
Пусть латинские буквы обозначают высказывания:
A - общеутвердительное;
E - общеотрицательное;
O - частноотрицательное;
I - частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | O | 3 |
Пусть латинские буквы обозначают высказывания:
A - общеутвердительное;
E - общеотрицательное;
O - частноотрицательное;
I - частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | E | 4 |
Пусть латинские буквы обозначают высказывания:
A - общеутвердительное;
E - общеотрицательное;
O - частноотрицательное;
I - частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| E | A | 4 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 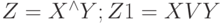 . (То есть:
. (То есть: 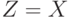 и
и  ;
;  или
или  .) Каково логическое значение выражения:
.) Каково логическое значение выражения:  и
и  .
.
 |  |
|---|---|
| 1 | 1 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 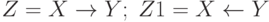 . Каково логическое значение выражения:
. Каково логическое значение выражения:  и
и  .
.
 |  |
|---|---|
| 0 | 1 |
Представьте формулу алгебры высказываний в дизъюнктивной нормальной форме:
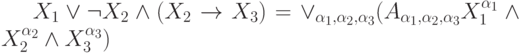
где
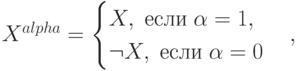
 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
| 1 | 1 | 0 |
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:
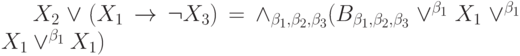
где
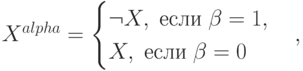
 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
| 1 | 1 | 1 |
Даны значения логических переменных  и значения их логических функций:
и значения их логических функций: 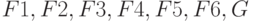 . Можно ли утверждать, что функция G не следует из функций
. Можно ли утверждать, что функция G не следует из функций 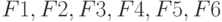 как из посылок. Да - 1. Нет - 0.
как из посылок. Да - 1. Нет - 0.
 |  |  |  |  |  |  |  |  |  |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 |
Проверьте справедливость утверждающе отрицающего модуса 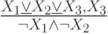
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 0 | 0 | 1 |
Проверьте справедливость утверждающе отрицающего модуса 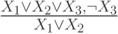
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 0 | 1 | 0 |
Проведите сложение двух пятизначных двоичных слагаемых:  .
.
В ответе приведите значение второго слагаемого в десятичной форме.
Заданы три функции:
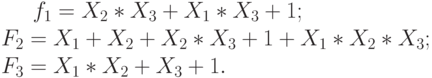
Функция 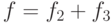 .
.
Проверьте, является ли она сохраняющей ноль.
Если да, то 1, если нет то 0.
Проверьте справедливость утверждающе отрицающего модуса 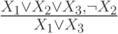
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 0 | 1 | 1 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 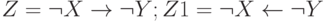 . Каково логическое значение выражения:
. Каково логическое значение выражения:  и
и  .
.
 |  |
|---|---|
| 1 | 1 |
Проверьте справедливость утверждающе отрицающего модуса 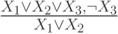
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 1 | 1 | 0 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 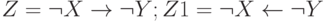 . Каково логическое значение выражения:
. Каково логическое значение выражения:  и
и  .
.
 |  |
|---|---|
| 0 | 1 |
Даны значения логических переменных  и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
 |  |  |  |  |  |  |  |  |  |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
Даны значения логических переменных  и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
 |  |  |  |  |  |  |  |  |  |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Даны значения логических переменных  и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
 |  |  |  |  |  |  |  |  |  |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 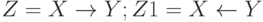 . Каково логическое значение выражения:
. Каково логическое значение выражения:  и
и  .
.
 |  |
|---|---|
| 1 | 1 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 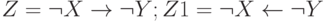 . Каково логическое значение выражения:
. Каково логическое значение выражения:  и
и  .
.
 |  |
|---|---|
| 0 | 0 |
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
Первый и последний президент СССР - М.С. Горбачёв. Москва - столица СССР. Следовательно, М.С. Горбачёв не проживает в Москве.
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 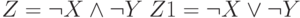 . Каково логическое значение выражения:
. Каково логическое значение выражения:  .
.
 |  |
|---|---|
| 0 | 1 |
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
Все кошки хищники. Хищники питаются убитыми ими животными. Кошка, поедающая украденные со стола куриные окорока, убила всех этих птиц.
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
Млекопитающие кормят детей своим грудным молоком. Человек - млекопитающее. Доцент Бояршинов - человек. Следовательно, он кормит детей своей грудью.
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
 и
и 
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
1024 - это 2 в 10-й степени.
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
Волга впадает в Каспийское море.
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
Следующее выражение является высказыванием: "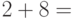 ".
".
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 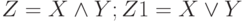 .Каково логическое значение выражения:
.Каково логическое значение выражения:  .
.
 |  |
|---|---|
| 1 | 1 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 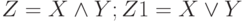 . Каково логическое значение выражения:
. Каково логическое значение выражения:  .
.
 |  |
|---|---|
| 0 | 1 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 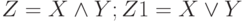 . Каково логическое значение выражения:
. Каково логическое значение выражения:  .
.
 |  |
|---|---|
| 0 | 0 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 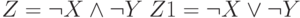 . Каково логическое значение выражения:
. Каково логическое значение выражения:  .
.
 |  |
|---|---|
| 1 | 1 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 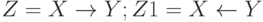 . Каково логическое значение выражения:
. Каково логическое значение выражения:  и
и  .
.
 |  |
|---|---|
| 0 | 0 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 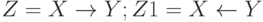 . Каково логическое значение выражения:
. Каково логическое значение выражения:  и
и  .
.
 |  |
|---|---|
| 0 | 1 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 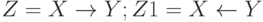 . Каково логическое значение выражения:
. Каково логическое значение выражения:  и
и  .
.
 |  |
|---|---|
| 1 | 1 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 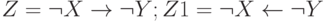 . Каково логическое значение выражения:
. Каково логическое значение выражения:  и
и  .
.
 |  |
|---|---|
| 0 | 0 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 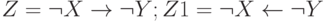 . Каково логическое значение выражения:
. Каково логическое значение выражения:  и
и  .
.
 |  |
|---|---|
| 0 | 1 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 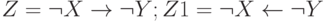 . Каково логическое значение выражения:
. Каково логическое значение выражения:  и
и  .
.
 |  |
|---|---|
| 1 | 0 |
Представьте формулу алгебры высказываний в дизъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 0 | 0 | 1 |
Представьте формулу алгебры высказываний в дизъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 0 | 1 | 0 |
Представьте формулу алгебры высказываний в дизъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 0 | 1 | 1 |
Представьте формулу алгебры высказываний в дизъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для  |  |  |
|---|---|---|
| 1 | 0 | 0 |
Представьте формулу алгебры высказываний в дизъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 1 | 0 | 1 |
Представьте формулу алгебры высказываний в дизъюнктивной нормальной форме:
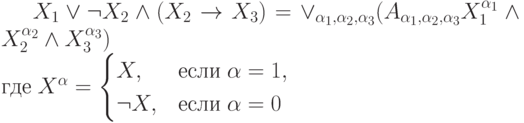
 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 1 | 1 | 0 |
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 0 | 0 | 0 |
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 0 | 0 | 1 |
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:
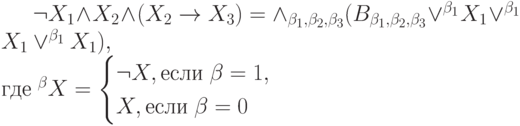
 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 0 | 1 | 1 |
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 1 | 0 | 1 |
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 1 | 1 | 0 |
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:
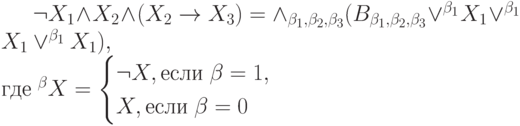
 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 1 | 1 | 1 |
Даны значения логических переменных  и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
 |  |  |  |  |  |  |  |  |  |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
Даны значения логических переменных  и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
 |  |  |  |  |  |  |  |  |  |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
Даны значения логических переменных  и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
 |  |  |  |  |  |  |  |  |  |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Проверьте справедливость утверждающе отрицающего модуса
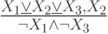
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 0 | 1 | 1 |
Проверьте справедливость утверждающе отрицающего модуса
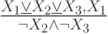
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 1 | 1 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
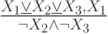
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 1 | 1 | 1 |
Проверьте справедливость утверждающе отрицающего модуса 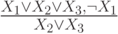
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 1 | 1 | 1 |
Проверьте справедливость утверждающе отрицающего модуса 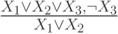
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 0 | 1 | 0 |
Проверьте справедливость утверждающе отрицающего модуса 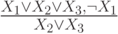
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 1 | 0 | 0 |
Проверьте справедливость утверждающе отрицающего модуса 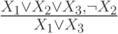
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 1 | 0 | 1 |
Проведите сложение двух пятизначных двоичных слагаемых:  .
.
В ответе приведите значение суммы в двоичной форме.
Проведите сложение двух пятизначных двоичных слагаемых:  .
.
В ответе приведите значение суммы в десятичной форме.
Заданы три функции:
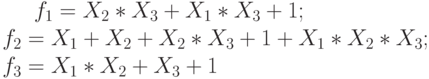
Функция 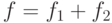 .
.
Проверьте, является ли она сохраняющей единицу.
Если да, то 1, если нет то 0.
Пусть латинские буквы обозначают высказывания:
A - общеутвердительное;
E - общеотрицательное;
O - частноотрицательное;
I - частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя, укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | I | 1 |
Пусть латинские буквы обозначают высказывания:
A - общеутвердительное;
E - общеотрицательное;
O - частноотрицательное;
I - частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| E | A | 1 |
Пусть латинские буквы обозначают высказывания:
A - общеутвердительное;
E - общеотрицательное;
O - частноотрицательное;
I - частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | E | 2 |
Пусть латинские буквы обозначают высказывания:
A - общеутвердительное;
E - общеотрицательное;
O - частноотрицательное;
I - частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| E | I | 2 |
Пусть латинские буквы обозначают высказывания:
A - общеутвердительное;
E - общеотрицательное;
O - частноотрицательное;
I - частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | A | 4 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 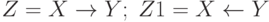 . Каково логическое значение выражения:
. Каково логическое значение выражения:  и
и  .
.
 |  |
|---|---|
| 0 | 1 |
Представьте формулу алгебры высказываний в дизъюнктивной нормальной форме:

где

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
| 1 | 1 | 0 |
Даны значения логических переменных  и значения их логических функций:
и значения их логических функций: 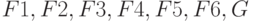 . Можно ли утверждать, что функция G не следует из функций
. Можно ли утверждать, что функция G не следует из функций 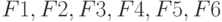 как из посылок. Да - 1. Нет - 0.
как из посылок. Да - 1. Нет - 0.
 |  |  |  |  |  |  |  |  |  |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
Проверьте справедливость утверждающе отрицающего модуса 
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 0 | 0 | 1 |
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 1 | 1 | 1 |
Заданы три функции:
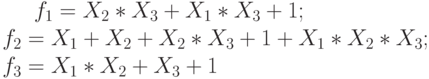
Функция 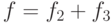 .
.
Проверьте, является ли она сохраняющей ноль.
Если да, то 1, если нет то 0.
Представьте формулу алгебры высказываний в дизъюнктивной нормальной форме:
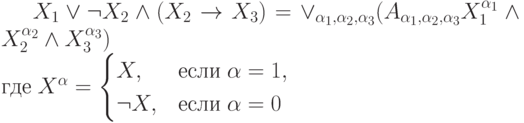
 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 1 | 0 | 0 |
Представьте формулу алгебры высказываний в дизъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 1 | 1 | 0 |
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:
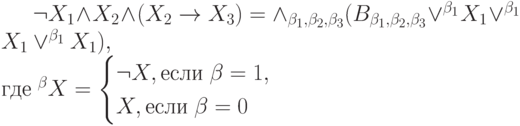
 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 1 | 0 | 1 |
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 0 | 0 | 0 |
Проверьте справедливость утверждающе отрицающего модуса 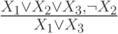
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 1 | 0 | 0 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 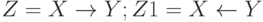 . Каково логическое значение выражения:
. Каково логическое значение выражения:  и
и  .
.
 |  |
|---|---|
| 0 | 0 |
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
Алюминий плотнее свинца.
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 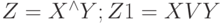 . (То есть:
. (То есть: 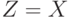 и
и  ;
;  или
или  .) Каково логическое значение выражения:
.) Каково логическое значение выражения:  и
и  .
.
 |  |
|---|---|
| 1 | 1 |
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
Киты и львы млекопитающие. Киты пьют солёную воду, следовательно львы пьют пресную.
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
13 - простое число, как и его квадрат.
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 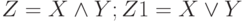 . Каково логическое значение выражения:
. Каково логическое значение выражения:  .
.
 |  |
|---|---|
| 1 | 0 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 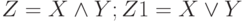 . Каково логическое значение выражения:
. Каково логическое значение выражения:  .
.
 |  |
|---|---|
| 0 | 1 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 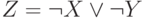 ;
;  . Каково логическое значение выражения:
. Каково логическое значение выражения:  .
.
 |  |
|---|---|
| 1 | 0 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 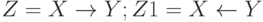 . Каково логическое значение выражения:
. Каково логическое значение выражения:  и
и  .
.
 |  |
|---|---|
| 0 | 1 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 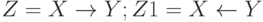 . Каково логическое значение выражения:
. Каково логическое значение выражения:  и
и  .
.
 |  |
|---|---|
| 1 | 0 |
Представьте формулу алгебры высказываний в дизъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 0 | 0 | 0 |
Представьте формулу алгебры высказываний в дизъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 1 | 1 | 1 |
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 0 | 1 | 0 |
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 0 | 1 | 1 |
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 1 | 0 | 0 |
Даны значения логических переменных  и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
 |  |  |  |  |  |  |  |  |  |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Даны значения логических переменных  и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
 |  |  |  |  |  |  |  |  |  |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
Даны значения логических переменных  и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
 |  |  |  |  |  |  |  |  |  |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 |
Даны значения логических переменных  и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
 |  |  |  |  |  |  |  |  |  |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
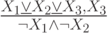
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 0 | 0 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
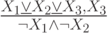
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 0 | 1 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
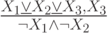
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 1 | 0 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
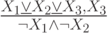
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 1 | 1 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
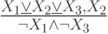
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 1 | 1 | 1 |
Проверьте справедливость утверждающе отрицающего модуса 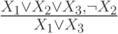
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 1 | 1 | 1 |
Проверьте справедливость утверждающе отрицающего модуса 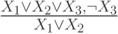
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 0 | 1 | 1 |
Проведите сложение двух пятизначных двоичных слагаемых:  .
.
В ответе приведите значение суммы в десятичной форме.
Проведите сложение двух пятизначных двоичных слагаемых:  .
.
В ответе приведите значение суммы в двоичной форме, ограничившись пятью младшими разрядами.
Проведите сложение двух пятизначных двоичных слагаемых:  ; ограничившись пятью младшими разрядами. В ответе приведите значение в десятичной форме.
; ограничившись пятью младшими разрядами. В ответе приведите значение в десятичной форме.
Пусть латинские буквы обозначают высказывания:
A - общеутвердительное;
E - общеотрицательное;
O - частноотрицательное;
I - частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | O | 2 |
Пусть латинские буквы обозначают высказывания:
A - общеутвердительное;
E - общеотрицательное;
O - частноотрицательное;
I - частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| E | I | 3 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 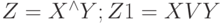 . (То есть:
. (То есть: 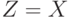 и
и  ;
;  или
или  .) Каково логическое значение выражения:
.) Каково логическое значение выражения:  и
и  .
.
 |  |
|---|---|
| 1 | 1 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 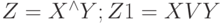 . (То есть:
. (То есть: 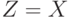 и
и  ;
;  или
или  .) Каково логическое значение выражения:
.) Каково логическое значение выражения:  и
и  .
.
 |  |
|---|---|
| 1 | 0 |
Представьте формулу алгебры высказываний в дизъюнктивной нормальной форме:
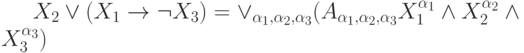
где

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
| 1 | 1 | 0 |
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:

где
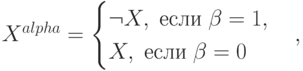
 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
| 1 | 1 | 1 |
Проверьте справедливость утверждающе отрицающего модуса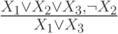
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 0 | 1 | 0 |
Заданы три функции:
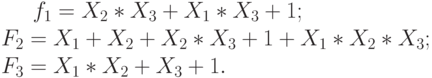
Функция 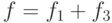 .
.
Проверьте, является ли она сохраняющей ноль.
Если да, то 1, если нет то 0.
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
В логике любое высказывание либо истинно, либо ложно.
Проведите сложение двух пятизначных двоичных слагаемых:  .
.
В ответе приведите значение второго слагаемого в десятичной форме.
Заданы три функции:
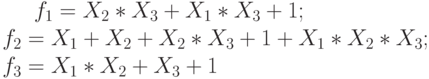
Функция 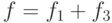 .
.
Проверьте, является ли она сохраняющей единицу.
Если да, то 1, если нет то 0.
Пусть латинские буквы обозначают высказывания:
A - общеутвердительное;
E - общеотрицательное;
O - частноотрицательное;
I - частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | A | 2 |
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
В Риме сохранились постройки времён Юлия Цезаря.
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 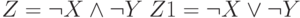 . Каково логическое значение выражения:
. Каково логическое значение выражения:  .
.
 |  |
|---|---|
| 0 | 0 |
Представьте формулу алгебры высказываний в дизъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 0 | 0 | 1 |
Представьте формулу алгебры высказываний в дизъюнктивной нормальной форме:
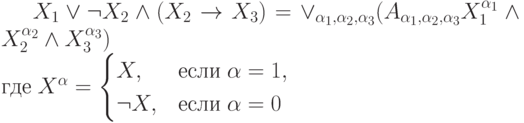
 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 1 | 0 | 1 |
Представьте формулу алгебры высказываний в дизъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 1 | 1 | 1 |
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:
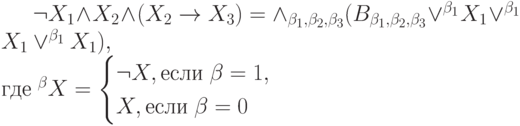
 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 0 | 0 | 1 |
Даны значения логических переменных  и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
 |  |  |  |  |  |  |  |  |  |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
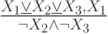
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 0 | 1 | 0 |
Проверьте справедливость утверждающе отрицающего модуса 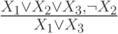
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 0 | 0 | 1 |
Проверьте справедливость утверждающе отрицающего модуса 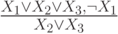
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 0 | 1 | 0 |
Проведите сложение двух пятизначных двоичных слагаемых:  ; ограничившись пятью младшими разрядами. В ответе приведите значение в десятичной форме.
; ограничившись пятью младшими разрядами. В ответе приведите значение в десятичной форме.
Заданы три функции:
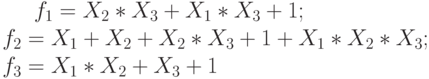
Функция 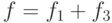 .
.
Проверьте, является ли она сохраняющей ноль.
Если да, то 1, если нет то 0.
Заданы три функции:
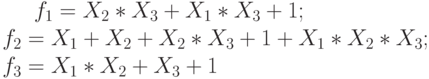
Функция 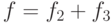 .
.
Проверьте, является ли она самодвойственной.
Если да, то 1, если нет то 0.
Пусть латинские буквы обозначают высказывания:
A - общеутвердительное;
E - общеотрицательное;
O - частноотрицательное;
I - частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | E | 1 |
Пусть латинские буквы обозначают высказывания:
A - общеутвердительное;
E - общеотрицательное;
O - частноотрицательное;
I - частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | I | 4 |
Пусть латинские буквы обозначают высказывания:
A - общеутвердительное;
E - общеотрицательное;
O - частноотрицательное;
I - частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| E | I | 4 |
Проверьте справедливость утверждающе отрицающего модуса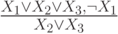
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 0 | 1 | 0 |
Даны значения логических переменных  и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
 |  |  |  |  |  |  |  |  |  |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 |
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 0 | 1 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
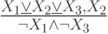
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 1 | 0 | 1 |
Представьте формулу алгебры высказываний в дизъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 0 | 1 | 0 |
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:
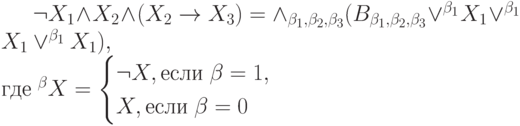
 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 1 | 1 | 0 |
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
Шесть делится на два без остатка и 7 - простое число.
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 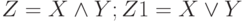 . Каково логическое значение выражения:
. Каково логическое значение выражения:  .
.
 |  |
|---|---|
| 0 | 0 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 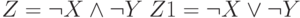 . Каково логическое значение выражения:
. Каково логическое значение выражения:  .
.
 |  |
|---|---|
| 1 | 0 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 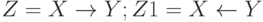 . Каково логическое значение выражения:
. Каково логическое значение выражения:  и
и  .
.
 |  |
|---|---|
| 1 | 0 |
Даны значения логических переменных  и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
 |  |  |  |  |  |  |  |  |  |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
Условия.
Даны значения логических переменных  и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
 |  |  |  |  |  |  |  |  |  |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
Проверьте справедливость утверждающе отрицающего модуса 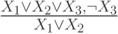
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 1 | 1 | 1 |
Проведите сложение двух пятизначных двоичных слагаемых:  .
.
В ответе приведите значение первого слагаемого в десятичной форме.
Проведите сложение двух пятизначных двоичных слагаемых:  .
.
В ответе приведите значение второго слагаемого в десятичной форме.
Заданы три функции:
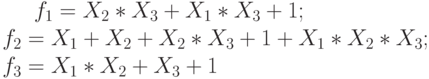
Функция 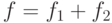 .
.
Проверьте, является ли она самодвойственной.
Если да, то 1, если нет то 0.
Даны значения логических переменных  и значения их логических функций:
и значения их логических функций: 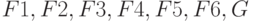 . Можно ли утверждать, что функция G не следует из функций
. Можно ли утверждать, что функция G не следует из функций 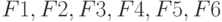 как из посылок. Да - 1. Нет - 0.
как из посылок. Да - 1. Нет - 0.
 |  |  |  |  |  |  |  |  |  |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
Проверьте справедливость утверждающе отрицающего модуса 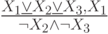
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 0 | 0 | 1 |
Пусть латинские буквы обозначают высказывания:
A - общеутвердительное;
E - общеотрицательное;
O - частноотрицательное;
I - частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| E | I | 1 |
Проверьте справедливость утверждающе отрицающего модуса 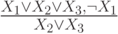
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 1 | 1 | 0 |
Заданы три функции:
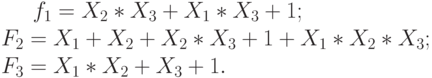
Функция 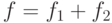 .
.
Проверьте, является ли она сохраняющей ноль.
Если да, то 1, если нет то 0.
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
Все хищники убивают своих жертв. Лев убил антилопу. Значит он хищник.
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 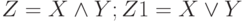 .Каково логическое значение выражения:
.Каково логическое значение выражения:  .
.
 |  |
|---|---|
| 1 | 0 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 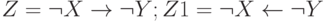 . Каково логическое значение выражения:
. Каково логическое значение выражения:  и
и  .
.
 |  |
|---|---|
| 1 | 1 |
Представьте формулу алгебры высказываний в дизъюнктивной нормальной форме:

 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 0 | 0 | 0 |
Представьте формулу алгебры высказываний в дизъюнктивной нормальной форме:
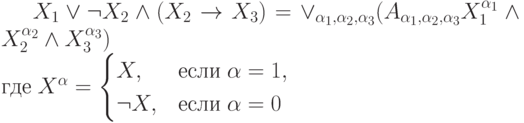
 может принимать значения 0 или 1. В ответе приведите значение
может принимать значения 0 или 1. В ответе приведите значение  для
для
 |  |  |
|---|---|---|
| 0 | 1 | 1 |
Проверьте справедливость утверждающе отрицающего модуса
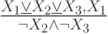
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 0 | 0 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
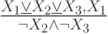
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 1 | 0 | 0 |
Проверьте справедливость утверждающе отрицающего модуса 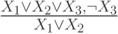
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 0 | 0 | 1 |
Проверьте справедливость утверждающе отрицающего модуса 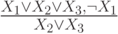
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 1 | 0 | 1 |
Проведите сложение двух пятизначных двоичных слагаемых:  .
.
В ответе приведите значение второго слагаемого в десятичной форме.
Пусть латинские буквы обозначают высказывания:
A - общеутвердительное;
E - общеотрицательное;
O - частноотрицательное;
I - частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | I | 3 |
Пусть латинские буквы обозначают высказывания:
A - общеутвердительное;
E - общеотрицательное;
O - частноотрицательное;
I - частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| E | A | 3 |
Как выглядит на языке кванторов утверждение: "Говорят, что предел последовательности с общим членом  равен
равен  , если для любого сколь угодно большого отрицательного числа (
, если для любого сколь угодно большого отрицательного числа (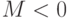 ) найдётся такой натуральный номер
) найдётся такой натуральный номер  , что все элементы последовательности с номерами, начиная с
, что все элементы последовательности с номерами, начиная с  , меньше
, меньше 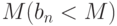 "
"
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 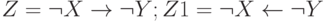 . Каково логическое значение выражения:
. Каково логическое значение выражения:  и
и  .
.
 |  |
|---|---|
| 1 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
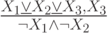
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 0 | 1 | 1 |
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
Шесть делится на три без остатка, поэтому оно простое число.
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 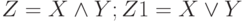 . Каково логическое значение выражения:
. Каково логическое значение выражения:  ?
?
 |  |
|---|---|
| 1 | 1 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 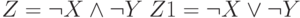 . Каково логическое значение выражения:
. Каково логическое значение выражения:  .
.
 |  |
|---|---|
| 0 | 1 |
Пусть  и
и  - высказывания (логические переменные). Их значения заданы в таблице.
- высказывания (логические переменные). Их значения заданы в таблице. 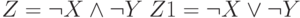 . Каково логическое значение выражения:
. Каково логическое значение выражения:  .
.
 |  |
|---|---|
| 1 | 1 |
Проведите сложение двух пятизначных двоичных слагаемых:  .
.
В ответе приведите значение суммы в двоичной форме.
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0: Волга в сердце впадает моё
Даны значения логических переменных  и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
и значения их логических функций: F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да - 1. Нет - 0.
 |  |  |  |  |  |  |  |  |  |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
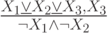
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 0 | 0 | 1 |
Проверьте справедливость утверждающе отрицающего модуса 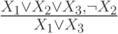
Определите: выполняются ли условия посылки для случая:
 |  |  |
| 0 | 0 | 0 |
Пусть латинские буквы обозначают высказывания:
A - общеутвердительное;
E - общеотрицательное;
O - частноотрицательное;
I - частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | A | 3 |

 "
" "
"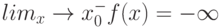 "
" "
"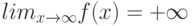 "
"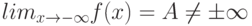 "
" "
"




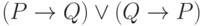
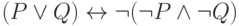
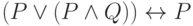
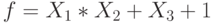 .
. .
.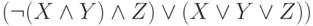
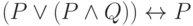
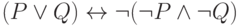
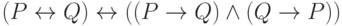

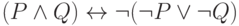
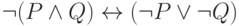
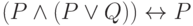
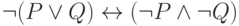
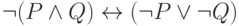



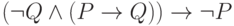
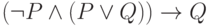
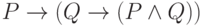
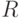


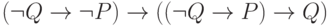
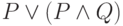

 . В качестве ответа введите 0 или 1.
. В качестве ответа введите 0 или 1.

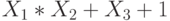 для значений:
для значений: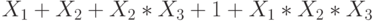 для значений:
для значений: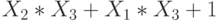 для значений:
для значений: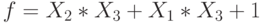 .
. .
.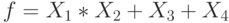 .
. .
.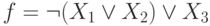 .
.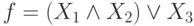 .
.
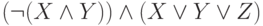
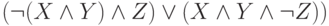

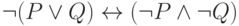
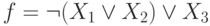 .
.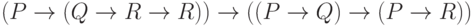
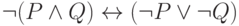
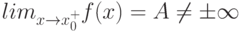 "
"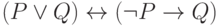

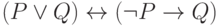
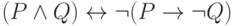

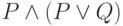
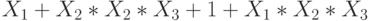 для значений:
для значений: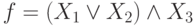 .
.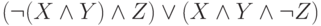
 "
"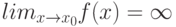 "
"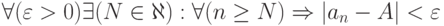 "
"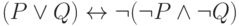
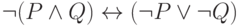

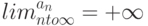 "
"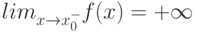 "
"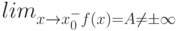 "
"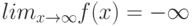 "
"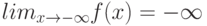 "
" "
"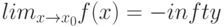 "
" "
"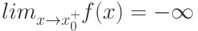 "
"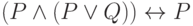
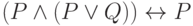
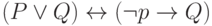
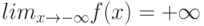 "
"