Пусть ряд 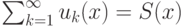 сходится равномерно на множестве
сходится равномерно на множестве  . Какие утверждения верны:
. Какие утверждения верны:
(Ответ считается верным, если отмечены все правильные варианты ответов.)
Варианты ответа
существует сходящийся числовой ряд 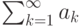 , для которого
, для которого 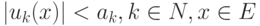
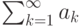 , для которого
, для которого 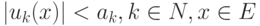
может не существовать сходящийся числовой ряд 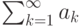 такой, что
такой, что 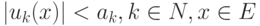 (Верный ответ)
(Верный ответ)
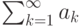 такой, что
такой, что 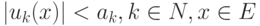 (Верный ответ)
(Верный ответ)
последовательность 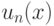 может не сходиться равномерно к
может не сходиться равномерно к  на
на 
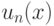 может не сходиться равномерно к
может не сходиться равномерно к  на
на 
последовательность 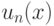 сходится равномерно к
сходится равномерно к  на
на  (Верный ответ)
(Верный ответ)
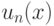 сходится равномерно к
сходится равномерно к  на
на  (Верный ответ)
(Верный ответ)

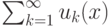 сходится равномерно к функции
сходится равномерно к функции  на множестве
на множестве  равномерно сходится к непрерывной
равномерно сходится к непрерывной  на множестве
на множестве  . Какие утверждения верны:
. Какие утверждения верны: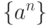 в пространстве
в пространстве 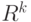 сходится и
сходится и 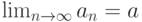 . Какие утверждения верны:
. Какие утверждения верны: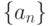 сходится и
сходится и  -множество частичных пределов
-множество частичных пределов  , дифференцируема на
, дифференцируема на 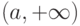 и
и  . Какие утверждения верны:
. Какие утверждения верны: