База ответов ИНТУИТ

Введение в математику. Практикум - ответы

Количество вопросов - 79

Функция y=f(x) называется непрерывной в точке x0∈D(f), если выполнено условие:

Метод, при котором реализуется схема А(n)→​A(n–1)→​…→​A(1) доказательства утверждения А(n), зависящего от натурального параметра n, называется:

Метод бисекции позволяет находить:

Предмет математики составляет, в основном, изучение связей и отношений:

Площадь фигуры, ограниченная линиями y=x,y=2–x2 равна:

Производная функции 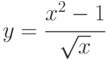y=\cfrac{x^2-1}{\sqrt{x}} в точке x=1 равна:

Связь полярных (ρ,ϕ) и декартовых (x,y) координат точки:

Дифференциальное уравнение – это уравнение, связывающее всегда значения:

Предел 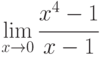\lim\limits_{x\rightarrow 0}\cfrac{x^4-1}{x-1}равен:

Интерполирование – это задача нахождения функции f(x), принимающей значение (значения) заданной табличной функции F(x):

Собственное число матрицы А(n×n) – это такое число с, для которого:

В матрице игры элементы отражают:

Если окружность растянуть (взяв за две точки на одном диаметре), то получим:

К мерам рассеяния относятся все указанные оценки:

Множество решений любой системы линейных неравенств на плоскости – это всегда:

Из утверждения: ∃ε>0 ∀δ>0: |Δx|=|x—x0|<δ⇒|Δy|=|f(x)—f(x0)|>ε следует факт:

40. Упорядочен по возрастанию ряд значений выражений:

Верны все включения вида:

Геометрическое место точек, отстоящих от начала координат на одинаковом расстоянии, равном 2, имеет уравнение:

Первообразная функции y=sin2x+cosx, график которой проходит через начало координат имеет вид:

Мировоззренческая роль математики позволяет нам (в основном):

Математика в современном мире применяется, в основном, для:

Связь декартовых (x,y) и полярных координат (ρ,ϕ) точки:

Геометрическое место точек, сумма расстояний каждой из которых до двух фиксированных точек постоянно, задает:

Число а – предел последовательности {xn}, если:

Метод, при котором реализуется схема А(1)→​A(n–1)→​A(n) доказательства утверждения А(n), зависящего от натурального параметра n, называется:

Ряд \sum\limits_{i=1}^{\infty}{a_i} называется сходящимся, если существует:

Целевая функция – это функция, для которой всегда ищем значение:

Среднее отражает закономерность:

Предел \lim\limits_{x\rightarrow\infty}\cfrac{x^3-1}{x^4+x-1} равен:

Производная функции 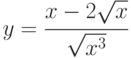y=\cfrac{x-2\sqrt{x}}{\sqrt{x^3}} в точке x=1 равна:

Первообразная функции y=sinx+cos2x, график которой проходит через начало координат имеет вид:

Упорядочен по возрастанию ряд значений выражений:

Число а – предел последовательности {xn}, если:

Верно включение одной числовой совокупности в другие числовые совокупности вида:

Производная функции y=sin3x+хcosx в точке x=0 равна:

В любом пространстве:

Радиус-вектор точки М(x,y,z) в декартовом пространстве представим разложением вида:

Число а называется пределом функции f(x) при x→​x0, x∈D(f), если выполнено условие:

Ряд \sum\limits_{i=1}^{\infty}{a_i} называется расходящимся, если:

Производной функции y=f(x) в точке x из области определения функции D(f) называется предел:

Геометрическое место точек, отстоящих от данной точки на одинаковом расстоянии, задает линию, называемую:

Множество возможных решений любой системы линейных неравенств в пространстве – это всегда:

К мерам оценки отклонений от среднего элемента в ряде относятся все указанные оценки:

Вектор 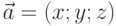\vec{a}=(x;y;z) представим разложением:

Интеграл \int\limits_1^2{\cfrac{2x^2+x-1}{x}dx}равен:

Производной функции y=f(x) в точке х=0 из области D(f) называется предел:

Произведение матриц A=\left\| \begin{array}{ccc}7&0&2\\2&3&1\end{array}\right\|и B=\left\| \begin{array}{cc}2&7\\3&0\\1&2\end{array}\right\| равно:

Интеграл 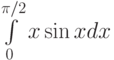\int\limits_{0}^{\pi/2}{x \sin x dx} равен:

Аппроксимирующая функция – функция f(x), принимающая значения заданной табличной функции F(x):

Математика в современном мире применяется (в основном) для:

Орграф – это граф, для которого:

Число а называется пределом последовательности {xn}, если выполнено условие:

Функция y=F(x)будет неопределенным интегралом для функции y=f(x), если:

Аппроксимация – задача нахождения функции f(x), принимающей значения заданной табличной функции F(x):

Предел \lim\limits_{x\rightarrow\infty}\cfrac{x^2-x+1}{x^2+3x}равен:

Функция y=f(x) называется непрерывной в точке x0∈D(f), если:

Предел 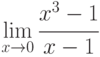\lim\limits_{x\rightarrow0}\cfrac{x^3-1}{x-1} равен:

Математика имеет основные ветви:

Евклидово, метрическое пространство – это пространство:

Площадь фигуры, ограниченная линиями y=x, y=x2 равна:

Интеграл 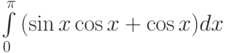\int\limits_0^{\pi}{(\sin{x}\cos{x}+\cos{x}) dx} равен:

Метод "золотого сечения" позволяет находить:

Интерполянта – функция f(x), принимающая значения заданной табличной функции F(x):

Производная функции y=xsinx+cos2x в точке x=0 равна:

Длина пути на графе – это:

Аббревиатура ЛПР означает:

Произведение матриц A=\left\| \begin{array}{ccc}1&0&2\\2&2&1\end{array}\right\|и B=\left\| \begin{array}{cc}2&3\\1&2\\1&0\end{array}\right\|равно:

Интеграл \int\limits_{0}^{\pi/2}{(\sin x\cos x +\sin x) dx} равен:

В линейном программировании:

Собственный вектор матрицы А(n×n) для собственного числа с– вектор х, для которого:

Интеграл \int\limits_0^1{xe^xdx} равен:

Матричной игрой называется игра с:

Функция y=F(x) называется первообразной для функции y=f(x), если выполнено условие:

Интеграл \int\limits_1^2{\cfrac{x^2+x+2}{x}dx} равен:

Неверно утверждение:

Воспитательная роль математики состоит в основном в том, что она позволяет:

Теорией игр называется:

Дифференциальное уравнение – это уравнение, связывающее значения: