Высшая математика на Mathcad - ответы
Количество вопросов - 114
Правильно ли заданы начальные значения для решения уравнения относительно переменной x при помощи функции root?

Какие из панелей инструментов используются для быстрого вызова справочной системы и электронных книг (примеров, учебников), встроенных в Mathcad? 
На рисунке приведен график распределения пар псевдослучайных величин X и Y. Каков их коэффициент корреляции? 
Какие функция в Mathcad могут применяться для решения одномерного волнового уравнения (в частных производных)?
Какая из представленных панелей используется для вставки в документ операторов интегрирования и дифференцирования? 
Рассмотрим решение линейного дифференциального уравнения  при помощи разностной схемы Эйлера
при помощи разностной схемы Эйлера  Какой порядок аппроксимации имеет эта схема?
Какой порядок аппроксимации имеет эта схема?


На рисунке приведен график распределения пар нормальных псевдослучайных величин X1 и X2? Чему (приблизительно) равны средние значения и дисперсии Х1 и Х2? Выберите все утверждения, которые считаете правильными. 
На рисунке приведен график распределения пар псевдослучайных величин X1 и X2. Как Вы думаете, какой закон распределения использовался в датчике псевдослучайных чисел? 
Какие из перечисленных функций предназначены для решения дифференциальных уравнений в частных производных?
Для решения краевых задач методом стрельбы применяется функция sbval(z,x0,x1,D,load,score). Какой из ее аргументов задает левые граничные условия?
Рассмотрим линейное одномерное уравнение теплопроводности: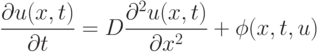 Шаблон для его решения изображен ниже. Явную или неявную схему описывает этот шаблон?
Шаблон для его решения изображен ниже. Явную или неявную схему описывает этот шаблон? 
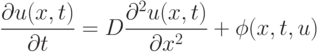
Ниже приведено решение краевой задачи для ОДУ 2-го порядка методом стрельбы. Одно условие поставлено на левой, другое – на правой границе интервала (0,1). Правильно ли определены аргументы-векторы load и score? 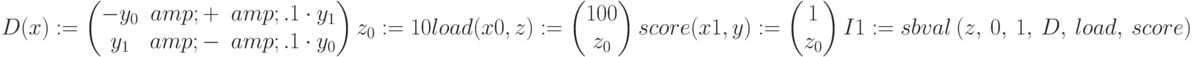
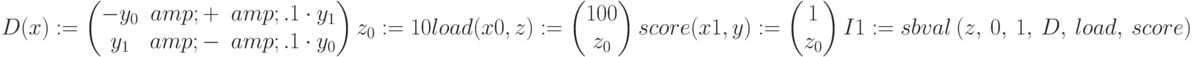
Правильно ли записан документ Mathcad для решения уравнения Пуассона с нулевыми граничными условиями и одним источником?
На рисунке показаны решения некоторого ОДУ тремя разными методами. Одни методы устойчивые, а другие – нет. Выберите неустойчивые решения? 
Какая из перечисленных функций используется для расчета значения среднеквадратичного отклонения элементов вектора х?
Какие из панелей инструментов используются для форматирования текста и формул (изменения типа и размера шрифта, выравнивания и т. п.)? 
Какой из параметров (флажков) надо изменить, чтобы иметь возможность вручную задать число меток разбиения шкалы координатной оси? 
Обязательно ли использование ключевого слова Given для определения системы уравнений при решении их встроенной функцией Find?
Что произойдет, если оператор символьного вывода заменить на знак равенства (т.е. на оператор численного вывода)? 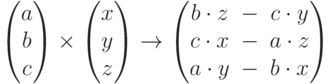
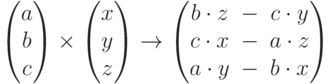
Рассмотрим решение линейного дифференциального уравнения  при помощи разностной схемы Эйлера
при помощи разностной схемы Эйлера  Какая это схема?
Какая это схема?


Рассмотрим (гипотетически, т.к. схема неустойчивая) решение линейного дифференциального уравнения  при помощи разностной схемы Эйлера
при помощи разностной схемы Эйлера  Какой порядок аппроксимации имеет эта схема?
Какой порядок аппроксимации имеет эта схема?


Для решения краевых задач методом стрельбы применяется функция sbval(z,x0,x1,D,load,score). Какой результат она выдает?
Рассмотрим линейное одномерное уравнение теплопроводности: 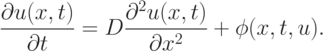 Шаблон для его решения изображен ниже. Явную или неявную схему описывает этот шаблон?
Шаблон для его решения изображен ниже. Явную или неявную схему описывает этот шаблон? 
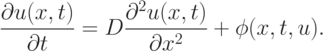
На рисунке приведен график распределения пар псевдослучайных величин X и Y. Каков их коэффициент корреляции? 
На рисунке приведен график распределения пар псевдослучайных величин X1 и X2. Как Вы думаете, какой закон распределения использовался в датчике псевдослучайных чисел? 
На рисунке приведен график распределения пар нормальных псевдослучайных величин X1 и X2? Чему (приблизительно) равны средние значения и дисперсии Х1 и Х2? Выберите все утверждения, которые считаете правильными. 
На рисунке изображен Фурье-спектр функции 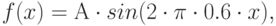 полученный при помощи БПФ. Пунктиром обозначена частота Найквиста. Правильно ли расположен пик спектра?
полученный при помощи БПФ. Пунктиром обозначена частота Найквиста. Правильно ли расположен пик спектра? 
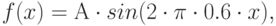
Какая из перечисленных функций используется для расчета плотности вероятности нормального распределения (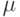 — математическое ожидание,
— математическое ожидание, 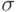 — среднеквадратичное отклонение)?
— среднеквадратичное отклонение)?
Будет ли осуществлено решение системы ОДУ осциллятора (достаточно ли параметров задано для его решения)?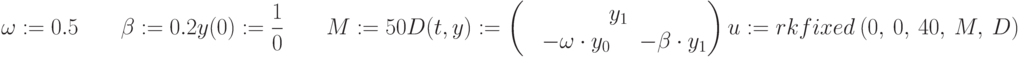
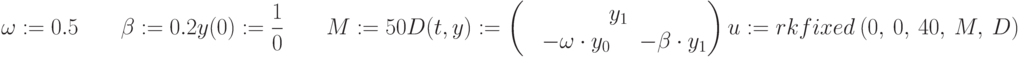
Для решения краевых задач методом стрельбы применяется функция sbval(z,x0,x1,D,load,score). Какой из ее аргументов задает систему ОДУ?
Какой из параметров (флажков) надо изменить, чтобы иметь возможность задать пределы диапазона оси координат? 
Обязательно ли использование ключевого слова Given для определения системы уравнений при решении их встроенной функцией root?
Какая из перечисленных функций используется для расчета обратной функции (квантиля) нормального распределения (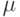 — математическое ожидание,
— математическое ожидание, 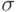 — среднеквадратичное отклонение)?
— среднеквадратичное отклонение)?
Ниже приведено решение краевой задачи для ОДУ 2-го порядка методом стрельбы. Одно условие поставлено на левой, другое – на правой границе интервала (0,1). Правильно ли определены аргументы-векторы load и score? 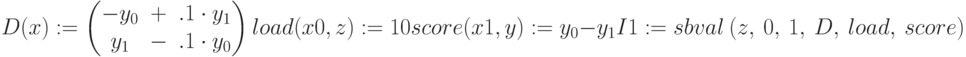
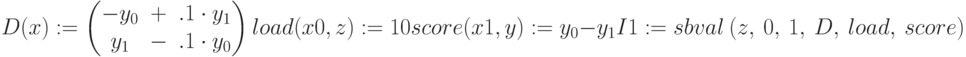
Для решения краевых задач методом стрельбы применяется функция sbval(z,x0,x1,D,load,score). Пусть система состоит из трех ОДУ, причем два условия поставлены на левой, а одно – на правой границе интервала. Какова размерность вектора load для правильной постановки задачи в Mathcad?
На рисунке изображен Фурье-спектр функции 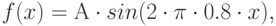 полученный при помощи БПФ. Пунктиром обозначена частота Найквиста. Правильно ли расположен пик спектра?
полученный при помощи БПФ. Пунктиром обозначена частота Найквиста. Правильно ли расположен пик спектра? 
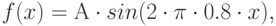
Какая из перечисленных функций используется для генерации вектора псевдослучайных чисел, имеющих нормальное распределение (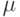 — математическое ожидание,
— математическое ожидание, 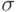 — среднеквадратичное отклонение)?
— среднеквадратичное отклонение)?
При помощи какой из панелей можно вызвать на экран (или скрыть) все остальные панели, показанные на рисунке? 
Сколько корней системы уравнений отыщет функция Find, если заменить в последней строке оператор символьного вывода (стрелку) на оператор численного вывода (знак равенства)?
Правильно ли заданы начальные значения для решения уравнения относительно переменной y при помощи функции root?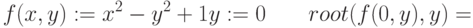
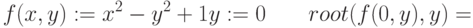
Рассмотрим решение линейного дифференциального уравнения  при помощи разностной схемы Эйлера
при помощи разностной схемы Эйлера 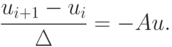 Какая это схема?
Какая это схема?

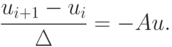
Рассмотрим решение линейного дифференциального уравнения  при помощи разностной схемы Эйлера
при помощи разностной схемы Эйлера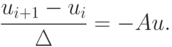 Какой порядок аппроксимации имеет эта схема?
Какой порядок аппроксимации имеет эта схема?

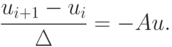
Будет ли осуществлено решение системы ОДУ осциллятора (достаточно ли параметров задано для его решения)?

Для решения краевых задач методом стрельбы применяется функция sbval(z,x0,x1,D,load,score). Пусть система состоит из трех ОДУ, причем два условия поставлены на левой, а одно – на правой границе интервала. Какова размерность вектора score для правильной постановки задачи в Mathcad?
Ниже приведено решение краевой задачи для ОДУ 2-го порядка методом стрельбы. Одно условие поставлено на левой, другое – на правой границе интервала (0,1). Правильно ли определены аргументы-векторы load и score?

Какая из перечисленных функций используется для расчета выборочного значения дисперсии элементов вектора х?
Обязательно ли использование ключевого слова Given при решении задачи оптимизации при помощи встроенной функцией minimize или maximize?
На рисунке приведен график распределения пар псевдослучайных величин X1 и X2. Как Вы думаете, какой закон распределения использовался в датчике псевдослучайных чисел? 
На рисунке приведен график распределения пар псевдослучайных величин X и Y. Каков их коэффициент корреляции? 
На рисунке приведен график распределения пар нормальных псевдослучайных величин X1 и X2? Чему (приблизительно) равны средние значения и дисперсии Х1 и Х2? Выберите все утверждения, которые считаете правильными. 
Какая из перечисленных функций используется для расчета выборочного среднего значения элементов вектора х?
Рассмотрим (гипотетически, т.к. схема неустойчивая) решение линейного дифференциального уравнения  при помощи разностной схемы Эйлера
при помощи разностной схемы Эйлера  Какая это схема?
Какая это схема?




![\begin{pmatrix}1\\2\\3\\\end{pmatrix}\cdot\begin{pmatrix}4\\5\\6\\\end{pmatrix}\cdot\begin{pmatrix}7\\8\\9\\\end{pmatrix}=\begin{pmatrix}224\\256\\288\\\end{pmatrix}\\\left[\begin{pmatrix}1\\2\\3\\\end{pmatrix}\cdot\begin{pmatrix}4\\5\\6\\\end{pmatrix}\right]\cdot\begin{pmatrix}7\\8\\9\\\end{pmatrix}=](https://intuit.ru//sites/default/files/tex_cache/51950f114939414b1d12aa8112a3de06.png)

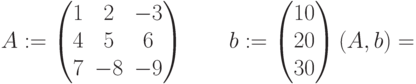

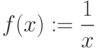

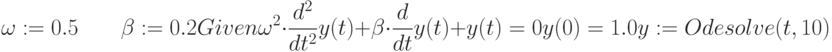
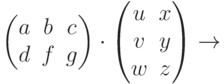
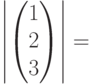


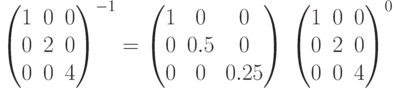


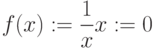



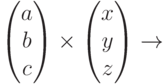
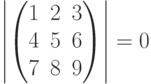


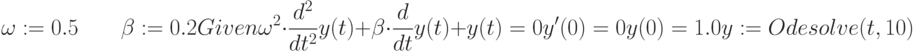

![L :=2 \cdot \pi \qquad T :=1\\Given\\v_t (x,t) = c^2 \cdot u_{xx}(x,t)\\u_t (x,t) = v (x,t)\\u(x,0) = sin \left(\frac{\pi \cdot x}{L} \right) \qquad v(x,0)=0\\u (0,t) = 0 \qquad u(L,t)=0\\\begin{pmatrix}u\\v\\\end{pmatrix} :=Pdesolve \left[\begin{pmatrix}u\\v\end{pmatrix},x,\begin{pmatrix}0\\L\\\end{pmatrix}, t,\begin{pmatrix}0\\T\\\end{pmatrix}\right]](https://intuit.ru//sites/default/files/tex_cache/abde126fc6166f0ab51e8ae0e0a9b15e.png)


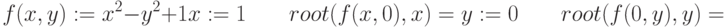
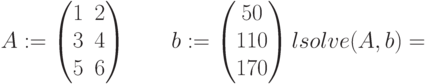
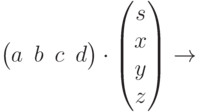

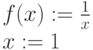



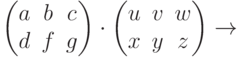
![D :=0.1\\L :=1 \qquad T :=10\\Given\\u_t (x,t) = D \cdot u_{xx}(x,t)\\u (x,0) = Ф (x -0.45) - Ф (x-0.55)\\u (0;t)=0 \qquad u (L,t) = 0\\u :=Pdesolve \left[ u,x, \begin{pmatrix}0\\L\end{pmatrix},t,\begin{pmatrix}0\\T\\\end{pmatrix}, 100, 10\right]](https://intuit.ru//sites/default/files/tex_cache/4a9d272a55e4fc6f7a9238cfcbe38c3c.png)




![\begin{pmatrix}1\\2\\3\\\end{pmatrix}\cdot\begin{pmatrix}4\\5\\6\\\end{pmatrix}\cdot\begin{pmatrix}7\\8\\9\\\end{pmatrix}=\begin{pmatrix}224\\256\\288\\\end{pmatrix}\\\begin{pmatrix}1\\2\\3\\\end{pmatrix}\cdot\left[\begin{pmatrix}4\\5\\6\\\end{pmatrix}\cdot\begin{pmatrix}7\\8\\9\\\end{pmatrix}\right]=](https://intuit.ru//sites/default/files/tex_cache/5759c760509c00e757eefca306541e9c.png)



