Основы теории информации и криптографии - ответы
Количество вопросов - 243
 Найти энтропию дискретной случайной величины X:
Найти энтропию дискретной случайной величины X:
Составить арифметический код для сообщения BAABC, полученного от дискретной случайной величины X со следующим распределением вероятностей P(X=A)=1/4, P(X=B)=1/2, P(X=C)=1/4:
 Найти среднюю длину code1 для дискретной случайной величины X:
Найти среднюю длину code1 для дискретной случайной величины X:
Коды с исправлением ошибок предназначены для:
Устройства для преобразования непрерывной информации в дискретную называются:
Нужно послать секретные сообщения 25 и 2 для JB и 14 для CIA, используя следующие записи открытой книги паролей криптосистемы RSA - JB: 77,7;CIA: 667,15
Считая, что код генерируется дискретной случайной величиной X с распределением P(X=A)=2/3, P(X=B)=1/3 вычислить длины кодов Хаффмена, блочного Хаффмена (для блоков длины 2 и 3) для сообщения ABAAAB:
Преимущество матричного кодирования заключается в:
Для кодирующей матрицы 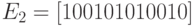 найти вероятность правильной передачи:
найти вероятность правильной передачи:
Преимущество арифметического кодирования позволяет:
Канал информационный представляет собой:
Общая схема передачи информации имеет вид:
Циклический избыточный код имеет:
Для кодирующей матрицы 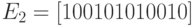 построить (3,4)-код:
построить (3,4)-код:
Выбрать верные утверждения:
Неравенством Варшамова - Гильберта называют выражение:
Вычислить ML(X) для кода Хаффмена для X. Дискретная случайная величина X задается следующим распределением вероятностей 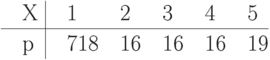 :
:
Передатчик задается случайной величиной со следующими законами распределениями вероятностей: P(X1=-1)=1/4, P(X1=0)=1/2, P(X1=1)=1/4. Емкость канала связи с шумом равна 4000 бод. Вычислить максимальную скорость передачи данных по этому каналу передатчиком, обеспечивающую сколь угодно высокую надежность передачи:
Закодировать сообщения "AABCDAACCCCDBB", вычислить длины в битах полученных кодов, используя алгоритм LZ77 (словарь - 12 байт, буфер - 4 байта):
Cообщение, полученное путем сжатия адаптивным алгоритмом Хаффмена с упорядоченным деревом имеет вид: 'A'0'F'00'X'0111110101011011110100101. Определить длину несжатого сообщения в битах:
Специальные таблицы для перевода неформальных данных в цифровой вид называются:
Основной категорией кибернетики является:
Первый БЧХ-код, примененный на практике, был:
Алгоритм DES предназначен для шифровки:
Алгоритм LZ77 выдает коды, состоящие из элементов:
Построить CRC-4 код для сообщения 10000000, используя полином-генератор x4+1:
Cжатие с потерями позволяет:
Предметом исследования кибернетики являются:
Сущность принципа управления заключается в том, что:
Дискретная информация характеризуется:
В таблице кодировки ASCII+ печатные и управляющие символы занимают:
Информация может быть нескольких типов:
Чем выше частота дискретизации, тем:
Устройства для преобразования дискретной информации в аналоговую называются:
Противоположность информации:
Общая схема передачи информации имеет вид:
Функция f-инъекция, если:
Значения дискретной случайной величины X1 и X2 определяются подбрасыванием двух идеальных монет, а дискретная случайная величина Y равна сумме количества "гербов", выпавших при подбрасывании этих монет. В Y содержится:
Определить HZ, если задана дискретная случайная величина Z=(X1+1)2-X2, где независимые дискретные случайные величины X1, X2 могут с равной вероятностью принимать значение либо 0, либо 1:
Дискретные случайные величины X1 и X2 определяются подбрасыванием двух идеальных тетраэдров, грани которых помечены числами от 1 до 4. Дискретная случайная величина Y равна сумме чисел, выпавших при подбрасывании этих тетраэдров, т.е. Y=X1+X2. Вычислить I(X1,Y):
Вычислить 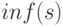 предложения
предложения 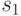 , про которое известно, что оно достоверно на 50%, и предложения
, про которое известно, что оно достоверно на 50%, и предложения 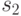 , достоверность которого 25%:
, достоверность которого 25%:
Если задана функция  , где s-это предложение, смысловое содержание которого измеряется, p(s) - вероятность истинности s, то если
, где s-это предложение, смысловое содержание которого измеряется, p(s) - вероятность истинности s, то если  :
:
 Найти среднюю длину code3 для дискретной случайной величины X:
Найти среднюю длину code3 для дискретной случайной величины X:
Про дискретную случайную величину X известно, что ее значениями являются буквы кириллицы. Произведен ряд последовательных измерений X, результат которых - "ТЕОРИЯИНФОРМАЦИИ". Составить на основании этого результата приблизительный закон распределения вероятностей этой дискретной случайной величины и оценить минимальную среднюю длину кодов для X:
Среднее количество бит, приходящихся на одно кодируемое значение дискретной случайной величины:
Выбрать верные утверждения:
Недостатками кодирования, основанного на основной теореме о кодировании при отсутствии помех, являются:
По методу Хаффмена код строится:
Вместе с собственно сообщением нужно передавать таблицу кодов для метода:
Вычислить ML(X) для кода Шеннона-Фэно для X. Дискретная случайная величина X задается следующим распределением вероятностей 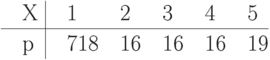 :
:
При кодировании методом Хаффмена и на 0 и на 1 придется тратить:
Дискретная случайная величина X может принимать три различных значения. При построении блочного кода с длиной блока 4 для X необходимо будет рассмотреть дискретную случайную величину X - выборку четырех значений X. X может иметь:
Закодировать сообщение "AABCDAACCCCDBB", используя адаптивный алгоритм Хаффмена с упорядоченным деревом:
Вычислить длины в битах сообщения "СИНЯЯ СИНЕВА СИНИ" в коде ASCII+ и его полученного кода
Распаковать сообщение 'A'0'F'00'X'0111110101011011110100101, полученное по адаптивному алгоритму Хаффмена с упорядоченным деревом
Популярность алгоритмов LZ обусловлена:
К недостаткам алгоритма LZ77 следует отнести:
Код, выдаваемый LZSS, начинается с:
Закодировать сообщения "СИНЯЯ СИНЕВА СИНИ", вычислить длины в битах полученных кодов, используя алгоритм LZW (словарь - ASCII+ и 16 фраз):
Закодировать сообщения "КИБЕРНЕТИКИ", вычислить длины в битах полученных кодов, используя алгоритм LZW (словарь - ASCII+ и 16 фраз):
Сжатие с потерями используется в основном для видов данных:
Сжатие видеоинформации основано на том, что:
Задержка сигнала во времени представляет собой:
По каналу связи без шума могут передаваться четыре сигнала длительностью 1 мс каждый. Вычислить емкость такого канала:
Передатчик задается случайной величиной со следующими законами распределениями вероятностей: P(X2=-1)=1/3, P(X2=0)=1/3, P(X_2=1)=1/3. Емкость канала связи с шумом равна 4000 бод. Вычислить максимальную скорость передачи данных по этому каналу передатчиком, обеспечивающую сколь угодно высокую надежность передачи:
Простой код с обнаружением ошибок основан на:
Расстоянием (Хэмминга) между двоичными словами длины n называется:
Следующее утверждение верно:
Имеется (8,9)-код с проверкой четности. Вычислить вероятность того, что в случае ошибки этот код ее не обнаружит, если вероятность ошибки при передаче каждого бита равна 0.1%:
Вычислить минимальную и максимальную оценки количества дополнительных разрядов r для кодовых слов длины n, если требуется, чтобы минимальное расстояние между ними было d. Рассмотреть случаи n = 32, d = 3 и n = 23, d = 7:
Блочный код называется групповым, если:
Двоичный блочный (m,n)-код называется оптимальным, если:
Для кодирующей матрицы  построить (2,5)-код:
построить (2,5)-код:
Для кодирующей матрицы 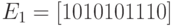 найти вероятность необнаружения ошибки:
найти вероятность необнаружения ошибки:
Для кодирующей матрицы  найти вероятность правильной передачи:
найти вероятность правильной передачи:
Построить кодовые слова квазисовершенного (9,n)-кода, исправляющего однократные ошибки, для тех сообщений, которые соответствуют числам 55, 200 и декодировать слова 1000001000001, 1100010111100, полученные по каналу связи, использующему этот код:
Способ построения полиномиальных кодов, минимальное расстояние между кодовыми словами которых равно заданному числу, был открыт:
Наиболее широкое распространение получил:
Для кода CRC-32 полином-генератор имеет степень:
Вычисление значения кода CRC происходит посредством:
Построить CRC-4 код для сообщения 10000000, используя полином-генератор x4+1:
Простейшая система шифрования основана на том, что:
Нераскрываемый шифр характеризуется тем, что:
Зашифровать сообщение "КИБЕРНЕТИКА" ключом "ДИСК":
Первая и наиболее известная система с открытым ключом называется:
Пользователь системы RSA выбрал p1=11 и p2=47. Некоторые числа из 12, 33, 125, 513 он может выбрать для открытого ключа. Вычислить для них закрытый ключ:
Самым распространенным типом данных в компьютерном мире является:
При логической разметке указывается:
Основными форматами текста с разметкой являются:
Большинство тегов языка HTML:
Атрибут ALT тега IMG используется для:
PostScript представляет собой:
Общая схема передачи информации имеет вид:
Древовидные коды также называют:
Системы с ключевым словом характеризуются тем, что:
Суть основной теоремы о кодировании при отсутствии помех заключается в том, что:
Последовательные коды характеризуются тем, что:
Бинарное дерево называется упорядоченным, если:
Дискретная случайная величина X задана распределением P(X=2n)=1/2n, n=1,2,..., Найти энтропию X:
Закодировать сообщение "СИНЯЯ СИНЕВА СИНИ", используя адаптивный алгоритм Хаффмена с упорядоченным деревом:
Стандарт LPC используется для:
При физической разметке точно указывается:
Кодирование, основанное на основной теореме о кодировании при отсутствии помех:
Вычислить минимальную оценку по Плоткину количества дополнительных разрядов r для кодовых слов матричного кода, если требуется, чтобы минимальное расстояние между ними было d. Рассмотреть случаи n = 32, d = 3 и n = 23, d = 7:
Дискретные случайные величины X1 и X2 определяются подбрасыванием двух идеальных тетраэдров, грани которых помечены числами от 1 до 4. Дискретная случайная величина Y равна сумме чисел, выпавших при подбрасывании этих тетраэдров, т.е. Y=X1+X2. Вычислить HY:
Если задана функция  , где s-это предложение, смысловое содержание которого измеряется, p(s) - вероятность истинности s, то эта функция обладает свойствами:
, где s-это предложение, смысловое содержание которого измеряется, p(s) - вероятность истинности s, то эта функция обладает свойствами:
Для кодирующей матрицы  найти минимальное расстояние между словами кода:
найти минимальное расстояние между словами кода:
Преимущество формата PostScript заключается в том, что:
Определить характер зависимости между X1 и Z, если задана дискретная случайная величина Z=(X1+1)2-X2, где независимые дискретные случайные величины X1, X2 могут с равной вероятностью принимать значение либо 0, либо 1:
Укажите свойства меры информации и энтропии:
Алгоритм DES предназначен для шифровки:
Специальные символы можно ввести в документ, используя их имена, заключенные между:
Собственно код, выдаваемый LZSS, состоит из:
Дискретная случайная величина X равна количеству "гербов", выпавших на двух идеальных монетках. Найти энтропию X:
Разделами кибернетики являются:
Теория информации представляет собой:
Информация может быть нескольких типов:
Суть теоремы о выборках заключается в том, что:
Кодирование представляет собой:
Если непрерывные случайные величины X, Y заданы плотностями распределения вероятностей pX(t1), pY(t2) и pXY(t1,t2), то количество информации, содержащейся в X относительно Y равно:
Вычислить 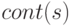 предложения s1, про которое известно, что оно достоверно на 50%, и предложения s2, достоверность которого 25%:
предложения s1, про которое известно, что оно достоверно на 50%, и предложения s2, достоверность которого 25%:
Если задана функция  , где s-это предложение, смысловое содержание которого измеряется, p(s) - вероятность истинности s, то:
, где s-это предложение, смысловое содержание которого измеряется, p(s) - вероятность истинности s, то:
 Найти среднюю длину code4 для дискретной случайной величины X:
Найти среднюю длину code4 для дискретной случайной величины X:
Выбрать верные утверждения:
Вместе с собственно сообщением нужно передавать таблицу кодов для метода:
Вычислить длины кодов Хаффмена и арифметического для сообщения AAB, полученного от дискретной случайной величины X со следующим распределением вероятностей P(X=A)=1/3, P(X=B)=2/3:
Закодировать сообщение "КИБЕРНЕТИКИ", используя адаптивный алгоритм Хаффмена с упорядоченным деревом:
Составить адаптивный арифметический код с маркером конца для сообщения BAABC:
Основная идея LZ77 состоит в том, что:
Алгоритм LZSS отличается от LZ77 следующим:
При чрезмерном увеличении размера словаря и буфера для алгоритмов LZ77 и LZSS, то это приведет:
Закодировать сообщения "AABCDAACCCCDBB", вычислить длины в битах полученных кодов, используя алгоритм LZ78 (словарь - 16 фраз):
Закодировать сообщения "КИБЕРНЕТИКИ", вычислить длины в битах полученных кодов, используя алгоритм LZSS (словарь - 12 байт, буфер - 4 байта):
Для сжатия графической информации с потерями в конце 80-х установлен стандарт:
Видеоинформацию можно сжать:
Эффективность канала характеризуется:
Имеется (8,9)-код с проверкой четности. Вычислить вероятность ошибочной передачи без использования кода, если вероятность ошибки при передаче каждого бита равна 1%:
Свойства совершенного кода могут быть представлены в виде:
Для кодирующей матрицы 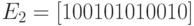 найти минимальное расстояние между словами кода:
найти минимальное расстояние между словами кода:
Коды Рида-Соломона являются:
При реальной передаче или хранении информации ошибки:
Построить CRC-4 код для сообщения 101111001, используя полином-генератор x4+1:
Между абонентами A и B установлен секретный канал связи без передачи ключей при заданных p=167 и их первых ключах 15 и 21. Описать процесс передачи сообщения 22 (от A к B):
Между абонентами A и B установлен секретный канал связи без передачи ключей при заданных p=167 и их первых ключах 15 и 21. Описать процесс передачи сообщения 17 (от B к A):
Пользователь системы RSA, выбравший p1=17, p2=11 и a = 61, получил шифрованное сообщение m1=3. Дешифровать m1:
World Wide Web базируется на стандартах:
К самодостаточным тегам языка HTML относятся:
Элементы SGML делятся на категории:
Алгоритм LZ77 выдает коды, состоящие из:
Бит определяет информацию:
CRC-коды способны обнаруживать:
Для печати документа на принтере или показе на экране используется:
Вычислить длины в битах сообщения "AABCDAACCCCDBB" в коде ASCII+ и его полученного кода
Дискретная случайная величина X может принимать три различных значения. Если считать сложность построения кода пропорциональной количеству различных значений кодируемой дискретной случайной величины, то блочный код для X по сравнению с неблочным сложнее строить в:
Канал связи представляет собой:
Принадлежат ли коду Голея кодовое слово 10000101011111010011111:
Если код является групповым, то:
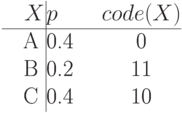 Вычислить ML1(X) для блочного кода Хаффмена для X. Длина блока - 2 бита:
Вычислить ML1(X) для блочного кода Хаффмена для X. Длина блока - 2 бита:
Причины, по которым документы PostScript сравнительно редко используются в WEB-страницах:
Вычислить длины в битах сообщения "КИБЕРНЕТИКИ" в коде ASCII+ и его полученного кода
Найти энтропию дискретной случайной величины X, заданной распределением 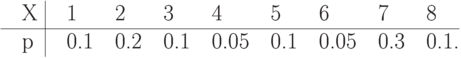
Словарные алгоритмы преимущественно отличаются от статистических тем, что:
Теория информации изучает:
При формальном представлении информации:
Частота дискретизации определяет:
Клод Шеннон предложил способ изменения количества информации:
Известно что  . Для каждого i pij равно либо qj, либо 0 при условии:
. Для каждого i pij равно либо qj, либо 0 при условии:
Определить HX1, если задана дискретная случайная величина Z=(X1+1)2-X_2, где независимые дискретные случайные величины X1, X_2 могут с равной вероятностью принимать значение либо 0, либо 1:
Энтропия дискретной случайной величины представляет собой:
Перед испытуемым человеком зажигается одна из N лампочек, которую он должен указать. Проводится большая серия испытаний, в которых каждая лампочка зажигается с определенной вероятностью pi, где i - это номер лампочки. Среднее время, необходимое для правильного ответа испытуемого, пропорционально:
Cообщение, полученное путем сжатия адаптивным алгоритмом Хаффмена с упорядоченным деревом имеет вид: 'A'0'F'00'X'0111110101011011110100101. Определить длину сжатого кода в битах:
Алгоритм LZ77 использует "скользящее" по сообщению окно, разделенное на две части, выполняющие определенные функции:
Сжатие с потерями обычно проходит в:
Простейший код для борьбы с шумом представляет собой:
Имеется (8,9)-код с проверкой четности. Вычислить вероятность того, что в случае ошибки этот код ее не обнаружит, если вероятность ошибки при передаче каждого бита равна 1%:
Имеется (8,9)-код с проверкой четности. Вычислить вероятность ошибочной передачи без использования кода, если вероятность ошибки при передаче каждого бита равна 0.1%:
Для кодирующей матрицы 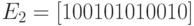 найти вероятность необнаружения ошибки:
найти вероятность необнаружения ошибки:
При полиномиальном кодировании каждое сообщение:
Способ построения полиномиальных кодов, минимальное расстояние между кодовыми словами которых равно заданному числу, был открыт:
Многочлен g(x) степени k называется примитивным, если:
Основными достоинствами DES являются:
Различают виды разметок текста:
К парным тегам языка HTML относятся:
LZ77 и LZSS обладают следующими очевидными недостатками:
Закодировать сообщение BBCBBC, используя адаптивный алгоритм Хаффмена с упорядоченным деревом:
Весом двоичного слова a=a1 ... a_n называется:
Дискретные случайные величины X1 и X2 определяются подбрасыванием двух идеальных тетраэдров, грани которых помечены числами от 1 до 4. Вычислить HX1.
Разметка текста позволяет:
"Скользящее" окно НЕ использует алгоритм:
Максимально плотно сжимает метод:
Полиномиальный код с кодирующим многочленом g(x) кодирует слово сообщения a(x) многочленом:
Сущность принципа управления заключается в том, что:
Информация может быть нескольких типов:
Чем ниже частота дискретизации, тем:
 Найти среднюю длину code2 для дискретной случайной величины X:
Найти среднюю длину code2 для дискретной случайной величины X:
Вместе с собственно сообщением нужно передавать таблицу кодов для метода:
Считая, что код генерируется дискретной случайной величиной X с распределением P(X=A)=2/3, P(X=B)=1/3 вычислить длину арифметического кода для сообщения ABAAAB:
Запатентованным является алгоритм:
Закодировать сообщения "СИНЯЯ СИНЕВА СИНИ", вычислить длины в битах полученных кодов, используя алгоритм LZ77 (словарь - 12 байт, буфер - 4 байта):
Коды с обнаружением ошибок предназначены для:
Найти кодирующий многочлен БЧХ-кода g(x) с длиной кодовых слов 15 и минимальным расстоянием между кодовыми словами 7. Использовать примитивный многочлен m1(x)=1+x+x4 с корнем  . Проверить, будут ли
. Проверить, будут ли  и
и 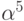 корнями соответственно многочленов m3(x)=1+x+x2+x3+x4 и m5(x)=1+x+x2:
корнями соответственно многочленов m3(x)=1+x+x2+x3+x4 и m5(x)=1+x+x2:
Проблема нераскрываемого шифра является:
Алгоритм DES предназначен для шифровки:
Устройства канала связи представляют собой:
Если дискретные случайные величины X и Y заданы законами распределения P(X=Xi)=pi, P(Y=Yj)=qj и совместным распределением P(X=Xi,Y=Yj)=pij, то количество информации, содержащейся в X относительно Y равно:
Аналоговая информация характеризуется:
Программа для АВМ представляет собой:
Префиксным называется кодирование:
Статистическими методами называют:
Простейший код, исправляющий ошибки представляет собой:
Передатчик задается случайной величиной со следующими законами распределениями вероятностей: P(X3=n)=2-n,\, n=1,2,... . Емкость канала связи с шумом равна 4000 бод. Вычислить максимальную скорость передачи данных по этому каналу передатчиком, обеспечивающую сколь угодно высокую надежность передачи:
Принадлежат ли коду Голея кодовое слово 11000111011110010011111:
Компьютерный шрифт представляет собой:
Особенностью системы с ключевым словом является:
Метод Шеннона-Фэно состоит в том, что:
Основной категорией кибернетики является:
Для кода CRC-16 полином-генератор имеет степень:
Вычислить HX для кодов Хаффмена и Шеннона-Фэно для X. Дискретная случайная величина X задается следующим распределением вероятностей 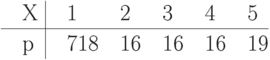 :
:
Основная идея сжатия графической информации с потерями заключается в том, что:
Составить арифметический код для сообщения BAABC, полученного от дискретной случайной величины X со следующим распределением вероятностей P(X=A)=1/3, P(X=B)=7/15, P(X=C)=1/5:

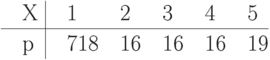 :
: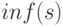 предложения
предложения 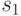 , про которое известно, что оно достоверно на 50%, и предложения
, про которое известно, что оно достоверно на 50%, и предложения 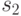 , достоверность которого 25%:
, достоверность которого 25%: , где s-это предложение, смысловое содержание которого измеряется, p(s) - вероятность истинности s, то если
, где s-это предложение, смысловое содержание которого измеряется, p(s) - вероятность истинности s, то если  :
: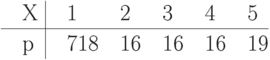 :
: , где s-это предложение, смысловое содержание которого измеряется, p(s) - вероятность истинности s, то эта функция обладает свойствами:
, где s-это предложение, смысловое содержание которого измеряется, p(s) - вероятность истинности s, то эта функция обладает свойствами: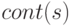 предложения s1, про которое известно, что оно достоверно на 50%, и предложения s2, достоверность которого 25%:
предложения s1, про которое известно, что оно достоверно на 50%, и предложения s2, достоверность которого 25%: , где s-это предложение, смысловое содержание которого измеряется, p(s) - вероятность истинности s, то:
, где s-это предложение, смысловое содержание которого измеряется, p(s) - вероятность истинности s, то: . Проверить, будут ли
. Проверить, будут ли  и
и 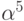 корнями соответственно многочленов m3(x)=1+x+x2+x3+x4 и m5(x)=1+x+x2:
корнями соответственно многочленов m3(x)=1+x+x2+x3+x4 и m5(x)=1+x+x2: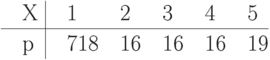 :
: