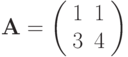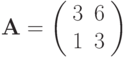База ответов ИНТУИТ

Элементы линейной алгебры для школьников - ответы

Количество вопросов - 106

При умножении вектора на действительное число С его длина

Определитель матрицы
\mathbf{A}=\left( \begin{array}{ccc}1 & 2 & 5 & \\2 & 4 & 6 & \\3 & 6 & 7 &\end{array} \right)
равен

Вектора x, y, z образуют ортонормированный базис, если

Результатом выполнения операции сложения двух векторов будет

В двумерном пространстве матрица поворота вектора на 180 градусов против часовой стрелки имеет вид

Алгебраические дополнения используются при

Результат умножения вектора на число

Для квадратной матрицы, все элементы которой равны 1, обратная матрицы

В системе линейных алгебраических уравнений АХ=В А - это

Если в перестановке число i расположено левее числа j, но i>j, то такая ситуация называется

Одна транспозиция в перестановке

Если А,B,С - матрицы, то операция А(B+C) эквивалентна операции

Согласно методу Гаусса для решения СЛАУ ее матрицу коэффициентов необходимо привести к

Пусть элементы последовательности формируются по правилу: fn+2=fn+1+2fn. Тогда для нахождения очередного элемента последовательности нужно умножить вектор
\mathbf{f}=\left( \begin{array}{c}f_{n+1} \\f_{n} \end{array} \right)
слева на матрицу А вида

После приведения матрицы
\mathbf{A}=\left( \begin{array}{cc}1 & 2 \\4 & 16 \end{array} \right)
к треугольному виду она будет иметь вид

Определитель диагональной или треугольной матрицы равен

Если в определителе поменять местами любые две строки, то он

Элементы пространства R3 можно представить в виде набора чисел:

Особенностью решения битовой СЛАУ методом Гаусса является

Для вычисления определителя произвольной матрицы с помощью метода Гаусса используется

Операция умножения матрицы на саму себя

Метод Гаусса используется для

Для матрицы
\mathbf{A}=\left( \begin{array}{cc}1 & 3 \\5 & 15 \end{array} \right)
обратная матрица равна

Алгебраические дополнение к элементу a11 матрицы
\mathbf{A}=\left( \begin{array}{cc}5 & 4 \\3 & 6 \end{array} \right)
равно

При программной реализации метода Гаусса решения СЛАУ матрица коэффициентов хранится в

Матрица А имеет 5 столбцов. Тогда для существования произведения матрицы А на матрицу B необходимо, чтобы B имела

Если элементы одного из стобцов (строки) определителя умножить на отличное от нуля действительное число, то

Пусть задана СЛАУ AX=B, где
\mathbf{A}=\left( \begin{array}{cc}1 & 1 \\3 & 4 \end{array} \right)
\mathbf{B}=\left( \begin{array}{c}5 \\6 \end{array} \right)
Тогда x1 равен

Равенство нулю скалярного произведения двух векторов означает их

Длина вектора равна нулю тогда и только тогда, когда этот вектор

Известно, что базис некоторого пространства составляют 4 вектора. Размерность такого пространства равна

Умножение вектора на число

Результатом сложения векторов x=(5;-3;2) и y=(1;2;1) будет вектор

Результатом умножения вектора x=(1;2;3) на число 2 будет

Результатом умножения матрицы
\mathbf{A}=\left( \begin{array}{cc}1 & 1 \\1 & 2 \end{array} \right)
на вектор
\mathbf{x}=\left( \begin{array}{c}1 \\1 \end{array} \right)
будет

Пусть элементы последовательности формируются по правилу: fn+2=2fn+1+fn. Тогда для нахождения очередного элемента последовательности нужно умножить вектор
\mathbf{f}=\left( \begin{array}{c}f_{n+1} \\f_{n} \end{array} \right)
слева на матрицу А вида

Для решения системы линейных уравнений методом Гаусса нужно привести матрицу системы

При программной реализации метода Гаусса решения СЛАУ вектор неизвестных хранится в

Время работы прямого хода метода Гаусса решения СЛАУ с m строк и n столбцов асимптотически составляет

Метод Гаусса

Определитель существует

Если в определителе поменять местами любые два столбца, то он

Если в определителе к элементам строки (столбца) прибавить одно и то же отличное от нуля действительно число, то

Если в определителе есть нулевая строка, то он равен

Матрица называется вырожденной, если

Определитель матрицы
\mathbf{A}=\left( \begin{array}{cc}1 & 2 \\3 & 4 \end{array} \right)
равен

Произведение матрицы на обратную к ней дает

Алгебраические дополнение к элементу a12 матрицы
\mathbf{A}=\left( \begin{array}{cc}5 & 4 \\3 & 6 \end{array} \right)
равно

Матрица, обратная для единичной матрицы

Для матрицы
\mathbf{A}=\left( \begin{array}{cc}1 & 1 \\1 & 2 \end{array} \right)
обратная матрица равна

Если на одном из этапов решения СЛАУ ищется определитель матрицы системы, в которой один из столбцов заменен на вектор свободных членов, то это означает, что СЛАУ решается методом

Пусть задана СЛАУ AX=B, где
\mathbf{A}=\left( \begin{array}{cc}1 & 1 \\3 & 4 \end{array} \right)
\mathbf{B}=\left( \begin{array}{c}5 \\6 \end{array} \right)
Тогда для нахождения x1 методом Крамера нужно найти определитель матрицы

В двумерном пространстве матрица поворота вектора на угол A имеет вид

Скалярное произведение ортогональных векторов равно

Из линейной независимости нескольких векторов

Если линейное многообразие содержит нулевой элемент, то оно является

В результате прямого хода метода Гаусса исходная матрица коэффициентов преобразуется к

Исходная матрица коэффициентов и приписанный к ней справа столбец свободных коэффициентов называется

Матрица называется невырожденной, если

Матрица А имеет 3 строки. Тогда для существования произведения матрицы B на матрицу A необходимо, чтобы B имела

Число четных перестановок

Результатом умножения матрицы
\mathbf{A}=\left( \begin{array}{cc}1 & 0 \\0 & 1 \end{array} \right)
на вектор
\mathbf{x}=\left( \begin{array}{c}5 \\6 \end{array} \right)
будет

В двумерном пространстве матрица поворота вектора на 90 градусов против часовой стрелки имеет вид

Любые 3 вектора пространства R2

Геометрически элементы пространства R1 представляются точками

Операция умножения матриц

В системе линейных алгебраических уравнений АХ=В Х- это

Время работы обратного хода метода Гаусса решения СЛАУ с m строк и n столбцов асимптотически составляет

Если в определителе две строки (столбца) равны, то

Пусть задана СЛАУ AX=B, где
\mathbf{A}=\left( \begin{array}{cc}1 & 1 \\3 & 4 \end{array} \right)
\mathbf{B}=\left( \begin{array}{c}5 \\6 \end{array} \right)
Тогда для нахождения x2 методом Крамера нужно найти определитель матрицы

Если в определителе две строки (столбца) линейно зависимы, то определитель равен

Обратная матрица имеет столько столбцов, сколько

Сдвиг линейного подпространства L на ненулевой вектор x дает

СЛАУ можно решить методом

Из попарной ортоногональности нескольких векторов следует

Результатом умножения вектора на число С будет

Операция умножения матриц аналогична операции

Для пространства R2 количество векторов в базисе равно

Результатом умножения матрицы
\mathbf{A}=\left( \begin{array}{cc}1 & 1 \\1 & 2 \end{array} \right)
на вектор
\mathbf{x}=\left( \begin{array}{c}1 \\1 \\1\end{array} \right)
будет

После приведения матрицы
\mathbf{A}=\left( \begin{array}{cc}1 & 2 \\3 & 4 \end{array} \right)
к треугольному виду она будет иметь вид

Особенностью битовой СЛАУ является то, что

Определитель матрицы - это

Если в определителе есть нулевая строка (столбец),то он равен

Определитель матрицы
\mathbf{A}=\left( \begin{array}{ccc}1 & 4 & 5 & \\0 & 2 & 6 & \\0 & 0 & 3 &\end{array} \right)
равен

Обратная матрица имеет столько строк, сколько

Определитель единичной матрицы равен

Для решения СЛАУ в матричном виде нужно

Длина суммы двух векторов

Для матрицы
\mathbf{A}=\left( \begin{array}{cc}1 & 1 \\3 & 4 \end{array} \right)
обратная матрица равна

Операция умножения двух матриц

После приведения матрицы
\mathbf{A}=\left( \begin{array}{cc}3 & 6 \\1 & 3 \end{array} \right)
к треугольному виду она будет иметь вид

Операция сложения векторов

Если размерность квадратной матрицы больше 3, то для вычисления ее определителя можно

Если А - исходная матрица коэффициентов, В - столбец свободных членов, Х - столбец неизвестных,то система линейных алгебраических уравнений (СЛАУ) в матричном виде запишется как

Каждому оператору отображения можно поставить в соответствие

Вектора x, y, z образуют базис. Следовательно, эти вектора

На первом шаге метода Гаусса решения СЛАУ

При программной реализации метода Гаусса решения СЛАУ возникают проблемы

Перестановка, в которой четное число инверсий, называется

Приведение матрицы к треугольному виду используется при решении систем линейных уравнений методом

Пусть элементы последовательности формируются по правилу: fn+2=fn+1+fn. Тогда для нахождения очередного элемента последовательности нужно умножить вектор
\mathbf{f}=\left( \begin{array}{c}f_{n+1} \\f_{n} \end{array} \right)
слева на матрицу А вида

Геометрически элементы пространства R2 представляются точками

Длина нулевого вектора равна

Если линейная комбинация векторов равна нулю, причем один из коэффициентов этой линейной комбинации отличен от нуля, то эти вектора

Если a - число; B,С - матрицы, то операция а(B+C) эквивалентна операции

При нахождении обратной матрицы нужно