Основы теории вычислимых функций - ответы
Количество вопросов - 264

h(x1,x2,…,xk,0) = f(x1,x2,…,xk,)h(x1,x2,…,xk,y+1) = g(x1,x2,…,xk,y,h(x1,x2,…,xk,y))называется:
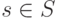 и читая символ
и читая символ  перейти в состояние для всех
перейти в состояние для всех  , напечатать символ
, напечатать символ 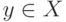 и сдвинуться влево" соответствует:
и сдвинуться влево" соответствует: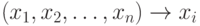 называют:
называют: