Введение в геометрическое программирование - ответы
Количество вопросов - 181
Для задачи ГП без ограничений запишите условие нормальности для двойственной задачи 
Коэффициенты позинома удовлетворяют условиям:
Для задачи ГП без ограничений запишите условия ортогональности для двойственной задачи 
Укажите число переменных в двойственной задаче 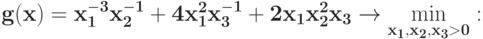
Наименьшее значение регулярного позинома равно
Вычислите минимальное значение позинома 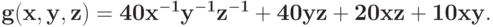
Преобразуйте в задачу ГП в каноническом виде задачу![\bf{\frac{[0.25 x_{1}^{3} + 6 x_{1}^{-4}x_{2}^{-2}]^{2.5}}{[4 x_{1}x_{2}^{3} - (2 x_{1}^{-2}x_{2}^{-1}+ 5 x_{1}^{-1})]^{4}} \rightarrow \min}](https://intuit.ru//sites/default/files/tex_cache/5ee303ade2f4e52c4116d9fd15202765.png) при ограничениях{
при ограничениях{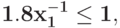 }{
}{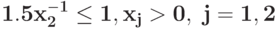 }
}
Уменьшите количество переменных в позиноме на две, выполнив последовательно 2 замены переменных(используйте теорему 3)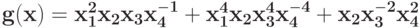
Вычислите верхнюю оценку минимума позинома 
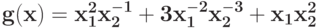 :
:
Преобразуйте в задачу ГП в каноническом виде задачу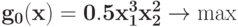 при ограничении
при ограничении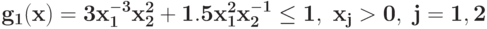
Укажите замену, которая уменьшает количество переменных в позиноме 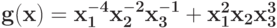
Решите следующую задачу, используя формулу, полученную в примере 16 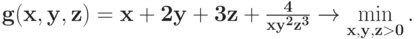
Преобразуйте в задачу ГП в каноническом виде задачу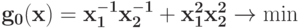 при ограничении
при ограничении
Укажите компоненты позинома и проверьте, является ли позином регулярным 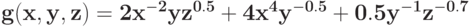
Запишите условия ортогональности для задачи 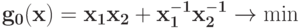 при ограничениях
при ограничениях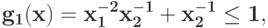

Запишите двойственную функцию для позинома 
Запишите двойственную функцию к задаче  при ограничениях
при ограничениях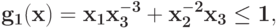
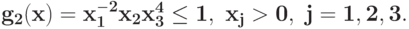
Преобразуйте в задачу ГП в каноническом виде задачу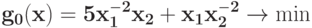 при ограничении
при ограничении
Если столбец 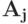 матрицы экспонент позинома
матрицы экспонент позинома является линейной комбинацией других столбцов, то
является линейной комбинацией других столбцов, то
Укажите замену, которая понижает количество переменных в позиноме, и вид позинома после этой замены 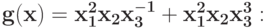
Запишите условие нормальности для задачи 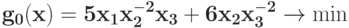 при ограничениях
при ограничениях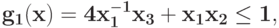
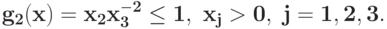
Ограничения задачи ГП в канонической форме имеют вид:
Верхней оценкой для минимума позинома является
Вычислите минимальное значение регулярного позинома 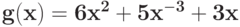 :
:
Укажите замену, которая уменьшает количество переменных в позиноме 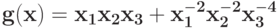
Задача ГП совместна, если:
Вычислите степень трудности для позинома (DOD) 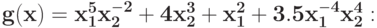
Неравенство Коши устанавливает, что среднееарифметическое  неотрицательных чисел
неотрицательных чисел
Укажите матрицу экспонент позинома 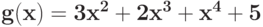 :
:
Геометрическое программирование - раздел математического программирования, в котором изучаются
Веса в обобщенном неравенстве Коши должны удовлетворять условию
Пусть функции  и
и 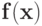 - позиномы, тогда
- позиномы, тогда
Укажите вектор коэффициентов позинома 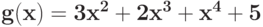 :
:
Укажите матрицу экспонент позинома 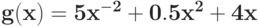 :
:
Укажите вектор коэффициентов позинома 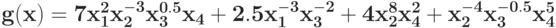 :
:
Укажите матрицу экспонент позинома 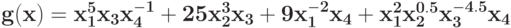 :
:
По вектору коэффициентов и матрице экспонент определитесоответствующий позином 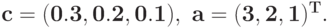 :
:
По вектору коэффициентов и матрице экспонент определитесоответствующий позином 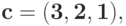
 :
:
Определите размерность задачи ГП без ограничений 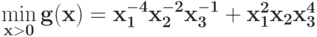
Определите размерность задачи ГП без ограничений 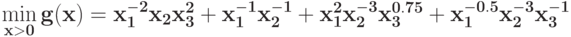
Укажите замену, которая понижает количество переменных в позиноме, и вид позинома после этой замены 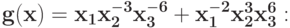
Укажите замену, которая уменьшает количество переменных в позиноме 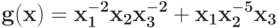
Решите следующую задачу, используя формулу, полученную в примере 16 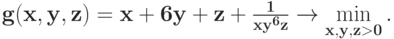
Решите следующую задачу, используя формулу, полученную в примере 16 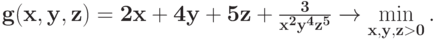
Позином является регулярным, если выполняются условия:
Позином является регулярным тогда и только тогда, когда
Нижней оценкой для минимума позинома является
Вычислите минимальное значение регулярного позинома 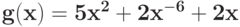 :
:
Вычислите верхнюю оценку минимума позинома 
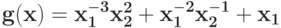 :
:
Укажите компоненты позинома и проверьте, является ли позином регулярным 
Условие нормальности в двойственной задаче имеет вид:
Переменные в двойственной задаче удовлетворяютусловию:
Для задачи ГП без ограничений запишите условия ортогональности для двойственной задачи 
Для задачи ГП без ограничений запишите условие нормальности для двойственной задачи 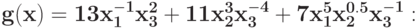
Укажите число переменных в двойственной задаче 
Вычислите минимальное значение позинома 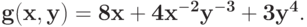
Вычислите степень трудности задачи ГП 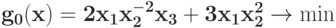 при ограничениях
при ограничениях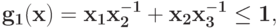

Запишите индексное множество  для задачи ГП
для задачи ГП 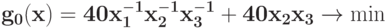 при ограничении
при ограничении 
Запишите матрицу экспонент  для задачи ГП
для задачи ГП 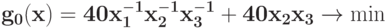 при ограничении
при ограничении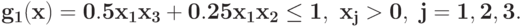
Запишите условия ортогональности для задачи  при ограничениях
при ограничениях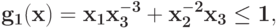
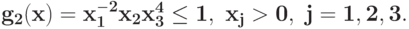
Запишите условие нормальности для задачи 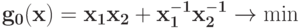 при ограничениях
при ограничениях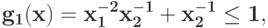

Укажите замену переменных, которая преобразует прямую задачу ГП в задачу выпуклого программирования:
Преобразуйте в задачу ГП в каноническом виде задачу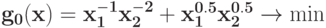 при ограничении
при ограничении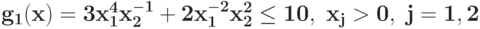
Преобразуйте в задачу ГП в каноническом виде задачу при ограничении
при ограничении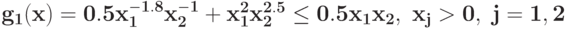
Преобразуйте в задачу ГП в каноническом виде задачу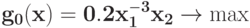 при ограничении
при ограничении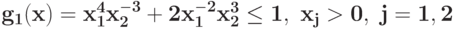
Преобразуйте в задачу ГП в каноническом виде задачу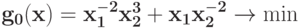 при ограничении
при ограничении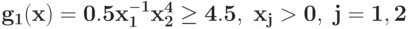
Преобразуйте в задачу ГП в каноническом виде задачу![\bf{\frac{[4 x_{1}x_{2} + 0. 5 x_{1}]^{4}}{[3 x_{1}^{3}x_{2}^{2} - (x_{1}^{-2}x_{2}^{-1}+ 5 x_{1}^{-1})]^{3}} \rightarrow \min}](https://intuit.ru//sites/default/files/tex_cache/d992d3f38fe1ba25f57e59952a2367a4.png) при ограничениях{
при ограничениях{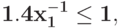 }{
}{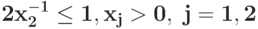 }
}
Геометрическим обратным мономом для позинома называется моном вида:
Вычислите степень трудности для позинома (DOD) 
Укажите замену, которая понижает количество переменных в позиноме, и вид позинома после этой замены 
Переменные позинома удовлетворяют условиям:
Двойственные переменные показывают, каков вклад вминимальное значение позинома
Преобразуйте в задачу ГП в каноническом виде задачу![\bf{\frac{[2 x_{1}^{-4} + 3 x_{1}^{3}x_{2}^{-2}+x_{2}^{7}]^{3}}{[2 x_{1}x_{2}^{6} - (0.5 x_{1}^{-2}x_{2}^{-1}+ 2 x_{1}^{-1})]^{1.5}} \rightarrow \min}](https://intuit.ru//sites/default/files/tex_cache/2a8abd08b63c86716e1ad8681e90dbd9.png) при ограничениях{
при ограничениях{ }{
}{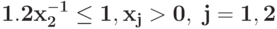 }
}
Регулярный позином всегда достигает наименьшего значения
Вычислите верхнюю оценку минимума позинома 
 :
:
Вычислите минимальное значение регулярного позинома 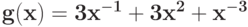 :
:
Укажите матрицу экспонент позинома 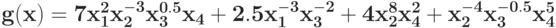 :
:
В задаче ГП вектор переменных 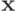 должен быть
должен быть
Укажите матрицу экспонент позинома 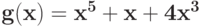 :
:
Укажите компоненты позинома и проверьте, является ли позином регулярным 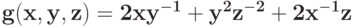
Гармоническим обратным позиномом для позиноманазывается позином вида:
Укажите замену, которая уменьшает количество переменных в позиноме 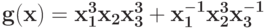
Запишите условия ортогональности для задачи 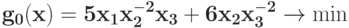 при ограничениях
при ограничениях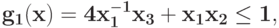
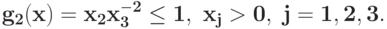
Преобразуйте в задачу ГП в каноническом виде задачу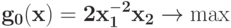 при ограничении
при ограничении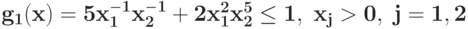
Решите следующую задачу, используя формулу, полученную в примере 16 
Уменьшите количество переменных в позиноме на две, выполнив последовательно 2 замены переменных(используйте теорему 3) 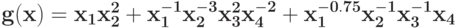
Определите размерность задачи ГП без ограничений 
По вектору коэффициентов и матрице экспонент определитесоответствующий позином 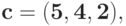
 :
:
Запишите матрицу экспонент  для задачи ГП
для задачи ГП  при ограничениях
при ограничениях
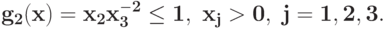
Регулярный позином достигает наименьшего значения
Вычислите минимальное значение позинома 
Укажите замену, которая понижает количество переменных в позиноме, и вид позинома после этой замены 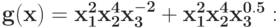
Когда в неравенстве Коши достигается равенство?
Пусть функции 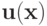 и
и 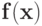 - мономы, тогда
- мономы, тогда
Компонентами позинома  являются позиномы
являются позиномы
Укажите вектор коэффициентов позинома 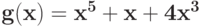 :
:
Укажите вектор коэффициентов позинома 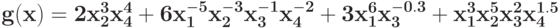 :
:
Укажите матрицу экспонент позинома 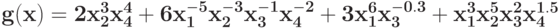 :
:
По вектору коэффициентов и матрице экспонент определитесоответствующий позином  :
:
Определите размерность задачи ГП без ограничений 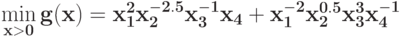
Укажите замену, которая уменьшает количество переменных в позиноме 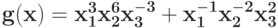
Уменьшите количество переменных в позиноме на две, выполнив последовательно 2 замены переменных(используйте теорему 3) 
Функции  и
и 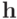 - регулярные позиномы, тогда функция
- регулярные позиномы, тогда функция
Вычислите верхнюю оценку минимума позинома 
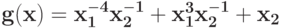 :
:
Укажите компоненты позинома и проверьте, является ли позином регулярным 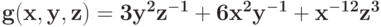
Вычислите степень трудности для позинома (DOD) 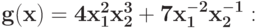
Для задачи ГП без ограничений запишите условия ортогональности для двойственной задачи 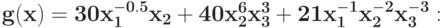
Для задачи ГП без ограничений запишите условие нормальности для двойственной задачи 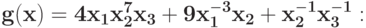
Вычислите минимальное значение позинома 
Вычислите степень трудности задачи ГП 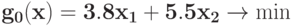 при ограничении
при ограничении
Запишите индексное множество 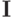 для задачи ГП
для задачи ГП 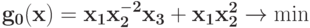 при ограничениях
при ограничениях 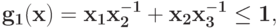

Запишите матрицу экспонент  для задачи ГП
для задачи ГП 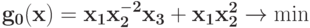 при ограничениях
при ограничениях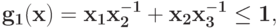

Запишите двойственную функцию к задаче  при ограничениях
при ограничениях 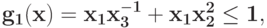

Запишите условие нормальности для задачи  при ограничениях
при ограничениях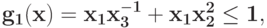

Преобразуйте в задачу ГП в каноническом виде задачу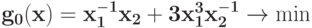 при ограничении
при ограничении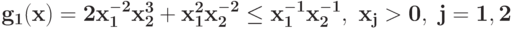
Сигном отличается от позинома тем, что:
Укажите число переменных в двойственной задаче 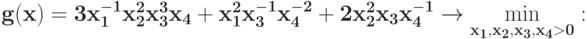
Преобразуйте в задачу ГП в каноническом виде задачу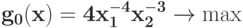 при ограничении
при ограничении
Запишите двойственную функцию к задаче  при ограничениях
при ограничениях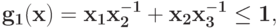
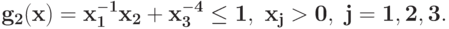
Для задачи ГП без ограничений запишите условия ортогональности для двойственной задачи 
Запишите индексное множество 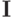 для задачи ГП
для задачи ГП  при ограничениях
при ограничениях 
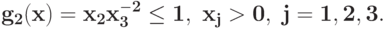
Укажите замену, которая понижает количество переменных в позиноме, и вид позинома после этой замены 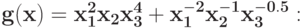
Запишите индексное множество 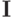 для задачи ГП
для задачи ГП 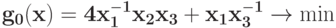 при ограничениях
при ограничениях 
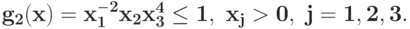
Процедуру понижения размерности задачи ГП можно выполнять
Условие ортогональности в двойственной задаче имеетвид:
Укажите число переменных в двойственной задаче 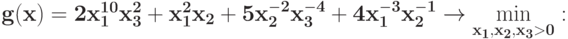
Какие из следующих функций являются мономами?
Вычислите минимальное значение регулярного позинома  :
:
Для задачи ГП без ограничений запишите условие нормальности для двойственной задачи 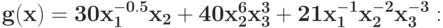
Укажите компоненты позинома и проверьте, является ли позином регулярным 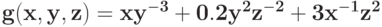
Запишите двойственную функцию для позинома 
Матрица экспонент позинома удовлетворяет условиям:
По вектору коэффициентов и матрице экспонент определитесоответствующий позином 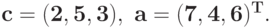 :
:
Уменьшите количество переменных в позиноме на две, выполнив последовательно 2 замены переменных(используйте теорему 3) 
Вычислите степень трудности для позинома (DOD) 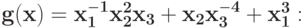
Запишите двойственную функцию для позинома 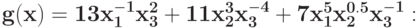
Для задачи ГП без ограничений запишите условие нормальности для двойственной задачи 
Запишите матрицу экспонент  для задачи ГП
для задачи ГП 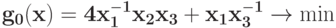 при ограничениях
при ограничениях
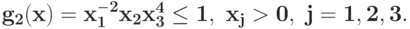
Запишите условие нормальности для задачи  при ограничениях
при ограничениях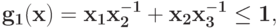
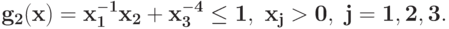
Преобразуйте в задачу ГП в каноническом виде задачу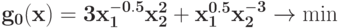 при ограничении
при ограничении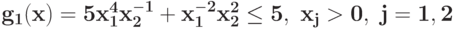
Преобразуйте в задачу ГП в каноническом виде задачу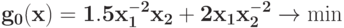 при ограничении
при ограничении
Преобразуйте в задачу ГП в каноническом виде задачу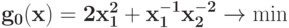 при ограничении
при ограничении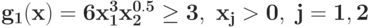
Преобразуйте в задачу ГП в каноническом виде задачу![\bf{\frac{[5 x_{1}^{2}x_{2}^{-1} + 3 x_{1}x_{2}^{-3}+ x_{1}]^{3}}{[2 x_{1}^{4}x_{2} - (x_{1}^{-2}x_{2}^{-1}+x_{1}^{-1})]^{2}} \rightarrow \min}](https://intuit.ru//sites/default/files/tex_cache/ce709ffbc930bf31d4be7c3e6543f37e.png) при ограничениях{
при ограничениях{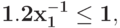 }{
}{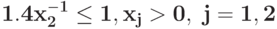 }
}
Вычислите степень трудности задачи ГП  при ограничении
при ограничении
По вектору коэффициентов и матрице экспонент определитесоответствующий позином 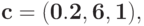
 :
:
Преобразуйте в задачу ГП в каноническом виде задачу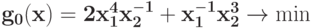 при ограничении
при ограничении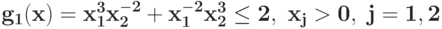
Определите размерность задачи ГП без ограничений 
Уменьшите количество переменных в позиноме на две, выполнив последовательно 2 замены переменных(используйте теорему 3) 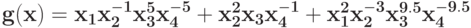
Укажите вектор коэффициентов позинома 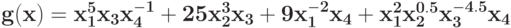 :
:
Значения переменных в двойственной задаче должны быть:
Решите следующую задачу, используя формулу, полученную в примере 16 
Укажите вектор коэффициентов позинома 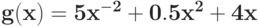 :
:
Число переменных в двойственной задаче ГП равно:
Вычислите степень трудности задачи ГП 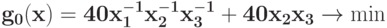 } при ограничении
} при ограничении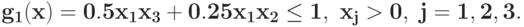
Запишите индексное множество 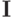 для задачи ГП
для задачи ГП 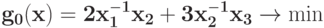 при ограничениях
при ограничениях 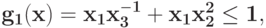

Запишите двойственную функцию к задаче 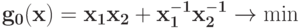 при ограничениях
при ограничениях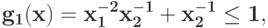

Преобразуйте в задачу ГП в каноническом виде задачу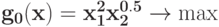 при ограничении
при ограничении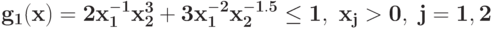
Запишите матрицу экспонент  для задачи ГП
для задачи ГП 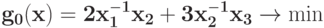 при ограничениях
при ограничениях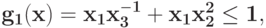

Запишите двойственную функцию для позинома 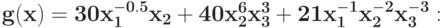
Вычислите степень трудности для позинома (DOD) 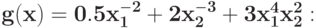
Запишите условия ортогональности для задачи  при ограничениях
при ограничениях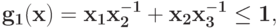
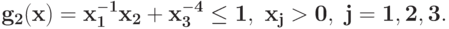
Вычислите верхнюю оценку минимума позинома 
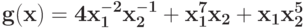 :
:
Вычислите степень трудности задачи ГП  при ограничениях
при ограничениях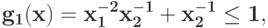
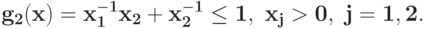
Преобразуйте в задачу ГП в каноническом виде задачу при ограничении
при ограничении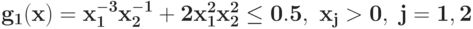
Преобразуйте в задачу ГП в каноническом виде задачу при ограничении
при ограничении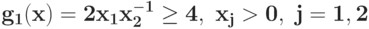
Преобразуйте в задачу ГП в каноническом виде задачу![\bf{\frac{[0.5 x_{1}^{-1}x_{2}^{-2} + 4 x_{2}]^{0.5}}{[0.5 x_{1}^{5}x_{2} - (4 x_{1}^{-2}x_{2}^{-1}+ x_{1}^{-1})]^{5}} \rightarrow \min}](https://intuit.ru//sites/default/files/tex_cache/c71c93eafe7c03d261f92218cde661b0.png) при ограничениях{
при ограничениях{ }{
}{ }
}
Для задачи ГП без ограничений запишите условия ортогональности для двойственной задачи 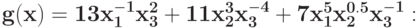
Укажите число переменных в двойственной задаче 
Вычислите минимальное значение позинома 
Запишите условия ортогональности для задачи  при ограничениях
при ограничениях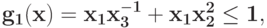

Запишите двойственную функцию для позинома 
Запишите условие нормальности для задачи  при ограничениях
при ограничениях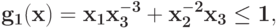
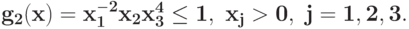
Обратная задача ГП, в отличие от задачи ГП канонического вида, имеет ограничения:
Вычислите минимальное значение регулярного позинома 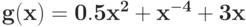 :
:
Преобразуйте в задачу ГП в каноническом виде задачу при ограничении
при ограничении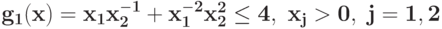
Преобразуйте в задачу ГП в каноническом виде задачу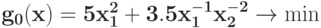 при ограничении
при ограничении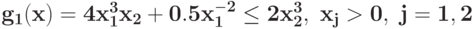
Функция  - регулярный позином.Функция
- регулярный позином.Функция  также регулярный позином при
также регулярный позином при  :
:
Запишите двойственную функцию к задаче 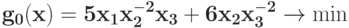 при ограничениях
при ограничениях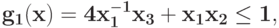
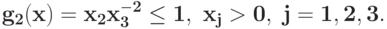
Преобразуйте в задачу ГП в каноническом виде задачу при ограничении
при ограничении