База ответов ИНТУИТ
заказать решение

Математический анализ. Интегральное исчисление - ответы

Количество вопросов - 100

Какие тригонометрические формулы можно использовать при вычислении интеграла 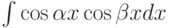\int\cos\alpha x\cos\beta xdx:

Чему равняется \int\frac{f'(x)}{\sqrt{f(x)}}dx?

Какая замена может использоваться при вычислении интеграла \int\frac{dx}{5+4\sin x}:

Пусть справедлива формула 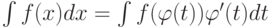\int f(x)dx=\int f(\varphi(t))\varphi'(t)dt замены переменных в неопределенном интеграле. Тогда

Разложите данную дробь 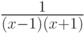\frac{1}{(x-1)(x+1)} на простейшие:

Требуется найти 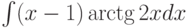\int(x-1)\arctg 2 xdx. Как применить формулу интегрирования по частям:

Отметьте верное равенство:

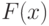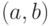Функция F(x) называется первообразной функции f(x) на интервале (a,b), если функция 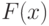F(x) дифференцируема

Какие из перечисленных дробей являются простейшими:

Отметьте верные утверждения:

Какая замена может использоваться при вычислении интеграла 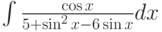\int\frac{\cos x}{5+\sin^2 x-6\sin x}dx:

Найдите первообразную для функции 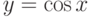y=\cos x, которая в точке 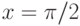x=\pi /2 принимает значение, равное 5

Каким методом можно вычислить интеграл 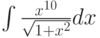\int\frac{x^{10}}{\sqrt{1+x^2}}dx

Какая замена может использоваться при вычислении интеграла \int\sin^{\alpha}x\cos^{2k+1}xdx:

Чему равняется интеграл от простейшей дроби 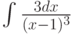\int\frac{3dx}{(x-1)^3}:

Пусть неправильная рациональная дробь представлена в виде 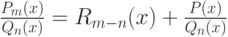\frac{P_m(x)}{Q_n(x)}=R_{m-n}(x) + \frac{P(x)}{Q_n(x)}. Тогда

Какая подстановка при вычислении 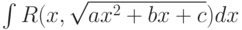\int R(x,\sqrt{ax^2+bx+c})dx является первой подстановкой Эйлера:

Отметьте верные утверждения:

Какую подстановку можно использовать для вычисления интеграла \int\frac{\sqrt{x}}{x+1}dx:

Через какую элементарную функцию будет выражаться интеграл 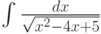\int\frac{dx}{\sqrt{x^2-4x+5}}:

Требуется найти 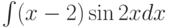\int(x-2)\sin 2xdx. Как применить формулу интегрирования по частям :

При вычислении интеграла 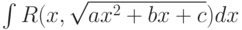\int R(x,\sqrt{ax^2+bx+c})dx вторая подстановка Эйлера применяется, если

Требуется найти \int\sqrt{4-x^2}dx для -2 \le x \le 2. Какая замена переменных допустима:

Какие функции являются рациональными от 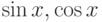\sin x,\cos x:

Пусть задана функция 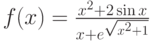f(x)=\frac{x^2+2\sin x}{x+e^{\sqrt{x^2+1}}}. Тогда функция f является рациональной от

Какая замена может использоваться при вычислении интеграла 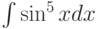\int\sin^5 xdx:

Отметьте верные равенства:

Какие элементарные функции могут быть в выражении для неопределенного интеграла от рациональных функций:

Требуется найти 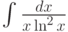\int\frac{dx}{x\ln^2 x}. Какая замена переменных целесообразна:

Какую подстановку можно применить при вычислении интеграла \int\frac{dx}{(x-2)\sqrt{-x^2+4x-3}}:

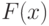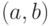Функция F(x) называется первообразной функции f(x) на интервале (a,b), если функция 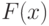F(x) дифференцируема

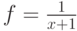Отметьте промежутки, на которых функция F=\ln(x+1) является первообразной для функции f=\frac{1}{x+1}:

Отметьте верные утверждения:

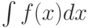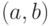Пусть \int f(x)dx - неопределенный интеграл от функции f на интервале (a,b). Тогда он

Отметьте верные равенства:

Какая формула является формулой замены переменных в неопределенном интеграле:

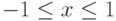Требуется найти для \int\sqrt{1-x^2}dx для -1\leq x\leq 1. Какая замена переменных допустима:

Требуется найти \int\frac{dx}{\sqrt[3]{x}+1}. Какая замена переменных целесообразна:

Чему равняется 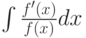\int\frac{f'(x)}{f(x)}dx?

Пусть справедлива формула \int udv=uv-\int vdu интегрирования по частям неопределенного интеграла. Какие утверждения верны:

Требуется найти 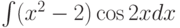\int(x^2-2)\cos 2xdx. Как применить формулу интегрирования по частям :

Перечислите множители, на которые раскладывается многочлен Q_n(x) с действительными коэффициентами:

Разложите данную дробь 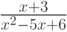\frac{x+3}{x^2-5x+6} на простейшие:

Отметьте верные утверждения:

Чему равняется интеграл от простейшей дроби 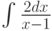\int\frac{2dx}{x-1}:

Какую подстановку можно использовать для вычисления интеграла \int\frac{1}{(x+2)^2}\sqrt[3]{\frac{x+1}{x+2}}dx:

Какая подстановка при вычислении 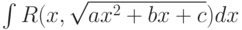\int R(x,\sqrt{ax^2+bx+c})dx является второй подстановкой Эйлера:

Отметьте верные утверждения:

Какую подстановку можно применить при вычислении интеграла  \int\frac{dx}{1+\sqrt{x^2+2x+2}}:

Через какую элементарную функцию будет выражаться интеграл \int\frac{dx}{\sqrt{6x-x^2}}:

Какие функции являются рациональными от 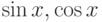\sin x,\cos x:

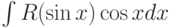Какая замена может использоваться при вычислении интеграла \int R(\sin x)\cos xdx:

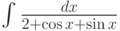Какая замена может использоваться при вычислении интеграла \int\frac{dx}{2+\cos x+\sin x}:

Какие тригонометрические формулы можно использовать при вычислении интеграла 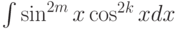\int\sin^{2m}x\cos^{2k}xdx:

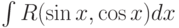Какая замена может использоваться при вычислении интеграла \int R(\sin x,\cos x)dx:

Отметьте верные равенства:

Пусть справедлива формула \int udv=uv-\int vdu интегрирования по частям неопределенного интеграла. Какие утверждения верны:

Каким методом можно вычислить интеграл \int\frac{2x^2+1}{\sqrt{x^2+2}}dx

Найдите первообразную для функции 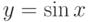y=\sin x, которая в точке 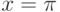x=\pi принимает значение, равное 8

Какие из перечисленных дробей являются простейшими

Пусть неправильная рациональная дробь представлена в виде 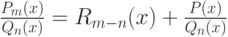\frac{P_m(x)}{Q_n(x)}=R_{m-n}(x) + \frac{P(x)}{Q_n(x)}. Тогда

Какие тригонометрические формулы можно использовать при вычислении интеграла \int\sin\alpha x\sin\beta xdx:

Какие элементарные функции могут быть в выражении для неопределенного интеграла от рациональных функций:

Разложите данную дробь 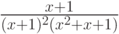\frac{x+1}{(x+1)^2(x^2+x+1)} на простейшие:

Отметьте верные равенства:

Какая замена может использоваться при вычислении интеграла 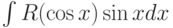\int R(\cos x)\sin xdx:

Отметьте верные утверждения:

Какие тригонометрические формулы можно использовать при вычислении интеграла 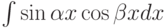\int\sin\alpha x\cos\beta xdx:

Какая замена может использоваться при вычислении интеграла \int\frac{dx}{2+\sin x}:

Отметьте промежутки, на которых функция 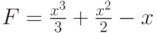F=\frac{x^3}{3}+\frac{x^2}{2}-x является первообразной для функции f=x^2+x-1:

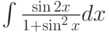Какая замена может использоваться при вычислении интеграла \int\frac{\sin 2x}{1+\sin^2 x}dx:

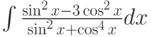Какая замена может использоваться при вычислении интеграла \int\frac{\sin^2 x-3\cos^2 x}{\sin^2 x+\cos^4 x}dx:

Какую подстановку можно использовать для вычисления интеграла 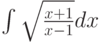\int\sqrt{\frac{x+1}{x-1}}dx:

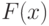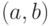Если функция F(x) является первообразной функции f(x) на интервале (a,b), то на этом интервале

Отметьте верные равенства:

Чему равняется 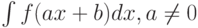\int f(ax+b)dx, a \neq 0, если F - первообразная функции f:

Требуется найти 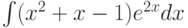\int(x^2+x-1)e^{2x}dx. Как применить формулу интегрирования по частям:

Чему равняется интеграл от простейшей дроби \int\frac{xdx}{x^2+x+1}:

Пусть задана функция f(x)=\frac{\sqrt{1-x^2}+2\sin^2 x}{x+2}. Тогда функция f является рациональной от

Какая подстановка при вычислении 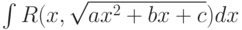\int R(x,\sqrt{ax^2+bx+c})dx является третьей подстановкой Эйлера:

Какая замена может использоваться при вычислении интеграла 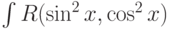\int R(\sin^2 x,\cos^2 x)dx:

Какая замена может использоваться при вычислении интеграла 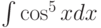\int\cos^5 xdx:

Каким методом можно вычислить интеграл 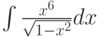\int\frac{x^6}{\sqrt{1-x^2}}dx

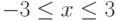Требуется найти для \int\sqrt{9-x^2}dx для -3\leq x\leq 3. Какая замена переменных допустима:

Отметьте верные утверждения:

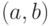Неопределенный интеграл от функции f на интервале (a,b) существует, если функция f

Требуется найти 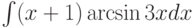\int(x+1)\arcsin 3 xdx. Как применить формулу интегрирования по частям:

Какую подстановку можно применить при вычислении интеграла \int\frac{dx}{\sqrt{x^2+1}}:

Требуется найти 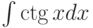\int\ctg xdx. Какая замена переменных целесообразна:

Найдите первообразную для функции 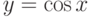y=\cos x, которая в точке x=0 принимает значение, равное 5

Отметьте верные утверждения:

Какая замена может использоваться при вычислении интеграла \int\frac{\sin 2x}{1+\cos^2 x}dx:

Через какую элементарную функцию будет выражаться интеграл 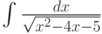\int\frac{dx}{\sqrt{x^2-4x-5}}:

Какие функции являются рациональными от 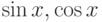\sin x,\cos x:

Требуется найти 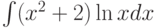\int(x^2+2)\ln xdx. Как применить формулу интегрирования по частям:

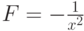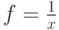Отметьте промежутки, на которых функция F=-\frac{1}{x^2} является первообразной для функции f=\frac{1}{x} :

При вычислении интеграла 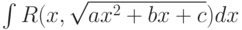\int R(x,\sqrt{ax^2+bx+c})dx первая подстановка Эйлера применяется, если

Какая формула является формулой интегрирования по частям:

Какие из перечисленных дробей являются простейшими:

Пусть задана функция 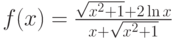f(x)=\frac{\sqrt{x^2+1}+2\ln x}{x+\sqrt{x^2+1}}. Тогда функция f является рациональной от