Введение в теорию множеств и комбинаторику - ответы
В букинистическом магазине лежат 6 экземпляров романа И.С. Тургенева "Рудин", 3 экземпляра его же романа "Дворянское гнездо" и 4 экземпляра романа "Отцы и дети". Кроме того, есть 5 томов, содержащих романы "Рудин" и "Дворянское гнездо", и 7 томов, содержащих романы "Дворянское гнездо" и "Отцы и дети". Сколькими способами можно сделать покупку, содержащую по 1 экземпляру каждого из этих романов?
Сколькими способами можно переставить буквы слова "бумага" так , чтобы буква "б" не шла непосредственно после буквы "у"?
У мамы 4 яблока и 3 груши. Каждый день в течении 5 дней подряд она выдаёт по одному фрукту. Сколькими способами это может быть сделано?
Сколькими способами можно переставить буквы слова "логарифм" так, чтобы ни одна буква не осталась на своем месте?
Сколькими способами можно посадить 4 мужчин и 4 женщин так, чтобы никакие 2 лица одного пола не сидели рядом на карусели и способы, переходящие друг в друга при вращении карусели, считаются совпадающими?
В продаже имеется 3 гуся, 4 курицы и 2 утки. Сколькими способами можно сделать покупку, включающую все три вида птиц?
Пусть множество  включает в себя корни уравнения
включает в себя корни уравнения  , а множество
, а множество  содержит значения
содержит значения 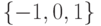 . Найти элементы множества
. Найти элементы множества 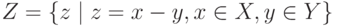 .
.
К какому типу относятся следующие множества? Представить элементы множеств в явном виде, если это возможно, и подсчитать мощность множеств.
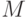 - множество гласных букв русского алфавита.
- множество гласных букв русского алфавита. - множество целых положительных нечетных чисел.
- множество целых положительных нечетных чисел. - множество двузначных чисел, являющихся степенями 2.
- множество двузначных чисел, являющихся степенями 2.Сколькими способами можно посадить за круглый стол 3 мужчин и 3 женщин так, чтобы никакие 2 лица одного пола не сидели рядом?
По результатам опроса студенческой группы из 32 человек 12 регулярно читают журнал "Мир ПК", 10 человек читают журнал "Открытые системы", 8 человек предпочитают журнал "Знание-сила", 3 человека читают и "Мир ПК" и "Открытые системы", 4 человека читают "Мир ПК" и "Знание-сила", 5 человек - "Открытые системы" и "Знание-сила", а 1 человек читает все три журнала. Сколько человек читают только "Мир ПК" ?
На собрании должно выступить 7 человек: А, Б, В, Г, Д , Е и Ж. Сколькими способами можно расположить их в списке ораторов при условии, что оратор А должен выступить непосредственно перед оратором В? Б не должен выступать до того, как выступит Д?
Сколько можно сделать перестановок из 6 элементов, в которых данные 2 элемента "А" и "Б" не стоят рядом?
Из 7 девушек и 5 юношей нужно создать 2 команды по 2 пары. Каждая пара включает соответственно девушку и юношу. Сколькими способами это можно сделать?
В классе 35 учащихся. Из них 20 посещают математический кружок, 11 - физический, 10 учащихся не посещают ни одного из этих кружков: сколько учащихся посещают только физический кружок?
В букинистическом магазине лежат 6 экземпляров романа И.С. Тургенева "Рудин" , 3 экземпляра его же романа "Дворянское гнездо" и 4 экземпляра романа "Отцы и дети". Кроме того, есть 5 томов, содержащих романы "Рудин" и "Дворянское гнездо", и 7 томов, содержащих романы "Дворянское гнездо" и "Отцы и дети", кроме того, в магазине есть 3 тома, в которые входят "Рудин" и "Отцы и дети". Сколькими способами можно сделать покупку, содержащую по 1 экземпляру каждого из этих романов?
Даны множества 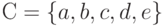 и
и 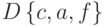 .
.
Найти мощности этих множеств. Является ли множество 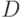 собственным подмножеством множества
собственным подмножеством множества  ?
?
К какому типу относятся следующие множества? Представить элементы множеств в явном виде, если это возможно, и подсчитать мощность множеств.
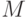 - множество нечетных чисел, больших 3 и меньших 10.
- множество нечетных чисел, больших 3 и меньших 10.  - множество целых положительных четных чисел.
- множество целых положительных четных чисел. - множество трехзначных чисел, являющихся степенями 2, которые нацело делятся на 5.
- множество трехзначных чисел, являющихся степенями 2, которые нацело делятся на 5.Пусть множество  включает в себя корни уравнения
включает в себя корни уравнения  , а множество
, а множество  содержит значения
содержит значения 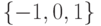 . Найти элементы множества
. Найти элементы множества 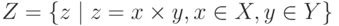 .
.
В классе 35 учащихся. Из них 20 посещают математический кружок, 11 - физический, 10 учащихся не посещают ни одного из этих кружков: сколько учеников посещают и математический и физический кружок?
Найти число целых положительных чисел, не превосходящих 300 и не делящихся ни на одно из чисел 2, 3 и 5.
По результатам опроса студенческой группы из 32 человек 12 регулярно читают журнал "Мир ПК", 10 человек читают журнал "Открытые системы", 8 человек предпочитают журнал "Знание-сила", 3 человека читают и "Мир ПК" и "Открытые системы", 4 человека читают "Мир ПК" и "Знание-сила", 5 человек - "Открытые системы" и "Знание-сила", а 1 человек читает все три журнала. Сколько человек читают только "Открытые системы"?
Даны множества 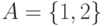 и
и 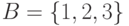 . a) записать элементы множества
. a) записать элементы множества 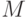 в явном виде, если
в явном виде, если 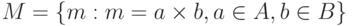 . б). записать элементы отношения
. б). записать элементы отношения 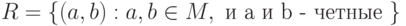 ; в). найти область определения
; в). найти область определения  и область значений
и область значений  .
.
Пусть имеется множество 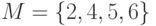 и задано отношение
и задано отношение 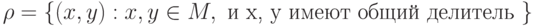 : a) записать отношение в явном виде; б)определить свойства отношения
: a) записать отношение в явном виде; б)определить свойства отношения  .
.
Пусть имеется множество 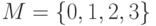 и задано отношение
и задано отношение  : a) записать отношение в явном виде; б) определить свойства отношения
: a) записать отношение в явном виде; б) определить свойства отношения  .
.
Пусть имеется множество  и задано отношение
и задано отношение 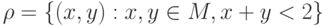 . Определить, какими свойствами обладает данное отношение.
. Определить, какими свойствами обладает данное отношение.
Пусть имеется множество 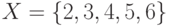 и задано отношение
и задано отношение  . Определить, какими свойствами обладает данное отношение.
. Определить, какими свойствами обладает данное отношение.
Пусть имеется множество  и задано отношение
и задано отношение  . Обладает ли данное отношение свойством эквивалентности?
. Обладает ли данное отношение свойством эквивалентности?
Сколько пятизначных чисел, которые одинаково читаются слева направо и справа налево (например, 67876,17071)?
Сколькими способами можно составить предложение, переставляя 3 слова: "мама" "мыла" "раму"?
Решение. Перестановки трех различных слов можно получить  способами, т. е. всего вариантов . . . . .
способами, т. е. всего вариантов . . . . .
Сколькими способами можно посадить 5 мужчин и 5 женщин так, чтобы никакие 2 лица одного пола не сидели рядом на карусели и способы, переходящие друг в друга при вращении карусели, считаются совпадающими?
Сколькими способами можно составить трехцветный полосатый флаг, если имеется материал 5 различных цветов при условии, что одна из полос должна быть красной?
На железнодорожной станции имеется m светофоров. Сколько может быть дано различных сигналов, если каждый светофор имеет 3 состояния: красный, желтый и зеленый?
У мамы 2 яблока и 3 груши. Каждый день в течении 5 дней подряд она выдаёт по одному фрукту. Сколькими способами это может быть сделано?
В продаже имеется 4 гуся, 3 курицы и 3 утки. Сколькими способами можно сделать покупку, включающую все три вида птиц?
В магазине имеется 60 музыкальных CD дисков и 30 дисков с фильмами. Можно купить 2 музыкальных диска или 3 диска с фильмами. В каком случае при покупке больше вариантов выбора?
В группе 27 человек. Необходимо сформировать команду из 4 человек. Сколькими способами это можно сделать?
Из 3 различных экземпляров учебника алгебры, 7 экземпляров учебника геометрии и 7 экземпляров учебника тригонометрии надо выбрать по одному экземпляру каждого учебника. Сколькими способами это можно сделать?
В букинистическом магазине лежат 5 экземпляров романа И.С. Тургенева "Рудин" , 4 экземпляра его же романа "Дворянское гнездо" и 2 экземпляра романа " Отцы и дети". Кроме того, есть 6 томов, содержащих романы "Рудин" и "Дворянское гнездо", и 5 томов, содержащих романы "Дворянское гнездо" и "Отцы и дети", кроме того, в магазине есть 3 тома, в которые входят "Рудин" и "Отцы и дети". Сколькими способами можно сделать покупку, содержащую по 1 экземпляру каждого из этих романов?
По результатам опроса студенческой группы из 32 человек 18 человек регулярно читает журнал "Мир ПК", 19 человек читают журнал "Открытые системы", 15 человек предпочитают журнал "Знание-сила", 8 человек читают и "Мир ПК" и "Открытые системы", 9 человек читают "Мир ПК" и "Знание-сила", 7 человек - "Открытые системы" и "Знание-сила", а 3 человека читает все три журнала. Сколько человек не читает ни одного из перечисленных журналов?
На потоке обучалось 65 студентов, все они посещали дисциплины по выбору, такие как "Теория графов", "Теория вероятности" и "Математическая статистика". Во время сессии "Теорию графов" успешно сдало 35 человек ; "Теорию вероятности" - 24 человека ; "Математическую статистику" - 22 чел. 8 - человек сдали "Теорию графов" и "Теорию вероятности", 7 человек - "Теорию графов" и "Мат. статистику", а 6 человек сдали "Теорию вероятности" и "Мат. статистику". 2 человека изучали все три дисциплины и успешно их сдали. Сколько человек не сдали экзамена ни по одной из перечисленных дисциплин?
На собрании должно выступить 5 человек: А, Б, В, Г и Д. Сколькими способами можно расположить их в списке ораторов при условии, что Б не должен выступать до того, как выступит А?
Сколько можно сделать перестановок из  элементов, в которых данные 2 элемента "А" и "Б" не стоят рядом?
элементов, в которых данные 2 элемента "А" и "Б" не стоят рядом?
На полке находятся 8 различных книг, из которых 3 в черных переплетах, а 5 в красных. Сколько существует перестановок этих книг, при которых книги в черных переплетах занимают первые три места?
Сколькими способами можно переставить буквы слова "кино" так, чтобы ни одна буква не осталась на своем месте?
Пусть имеется множество 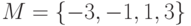 и задано отношение
и задано отношение 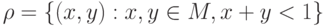 . Определить, какими свойствами обладает данное отношение.
. Определить, какими свойствами обладает данное отношение.
Пусть имеется множество 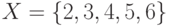 и задано отношение
и задано отношение 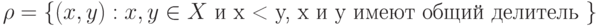 . Выписать все элементы
. Выписать все элементы  и представить
и представить  координатным способом.
координатным способом.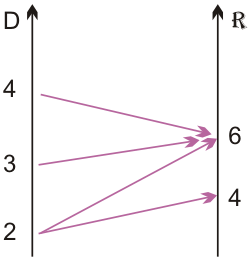
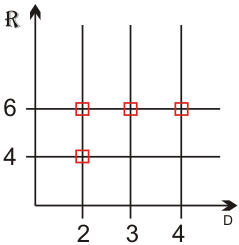
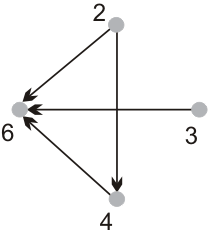
Даны множества 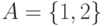 и
и 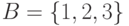 . a) записать элементы множества
. a) записать элементы множества 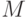 в явном виде, если
в явном виде, если 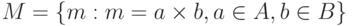 . б). записать элементы отношения
. б). записать элементы отношения 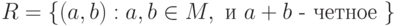 ; в). найти область определения
; в). найти область определения 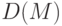 и область значений
и область значений 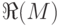 .
.
В магазине имеется 70 музыкальных CD дисков и 40 дисков с фильмами. Можно купить 2 музыкальных диска или 3 диска с фильмами. В каком случае при покупке больше вариантов выбора?
По результатам опроса студенческой группы из 32 человек 12 регулярно читают журнал "Мир ПК", 10 человек читают журнал "Открытые системы", 8 человек предпочитают журнал "Знание-сила", 3 человека читают и "Мир ПК" и "Открытые системы", 4 человека читают "Мир ПК" и "Знание-сила", 5 человек - "Открытые системы" и "Знание-сила", а 1 человек читает все три журнала. Сколько человек читают ровно два из названных журналов ?
Пусть имеется множество 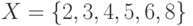 и задано отношение
и задано отношение  . Определить, какими свойствами обладает данное отношение.
. Определить, какими свойствами обладает данное отношение.
Пусть имеется множество 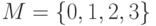 и задано отношение
и задано отношение 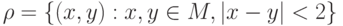 : a) записать отношение в явном виде; б) определить свойства отношения
: a) записать отношение в явном виде; б) определить свойства отношения  .
.
Сколькими способами можно переставить буквы слова "весна" так, чтобы ни одна буква не осталась на своем месте?
Из 5 различных экземпляров учебника алгебры, 4 экземпляров учебника геометрии и 6 экземпляров учебника тригонометрии надо выбрать по одному экземпляру каждого учебника. Сколькими способами это можно сделать?
Пусть имеется множество 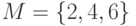 и задано отношение
и задано отношение 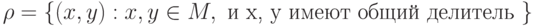 : a) записать отношение в явном виде; б)определить свойства отношения
: a) записать отношение в явном виде; б)определить свойства отношения  .
.
Даны множества 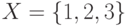 и
и 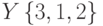 . Равны ли они?
. Равны ли они?
Записать элементы множества  , равного множествам
, равного множествам  и
и  .
.
Сколько вариантов записи множества  существует?
существует?
В классе 35 учащихся. Из них 20 посещают математический кружок, 11 - физический, 10 учащихся не посещают ни одного из этих кружков: сколько учащихся посещают только математический кружок?
На потоке обучалось 65 студентов, все они посещали дисциплины по выбору, такие как "Теория графов", "Теория вероятности" и "Математическая статистика". Во время сессии "Теорию графов" успешно сдали 31 человек ; "Теорию вероятности" - 27 человек ; "Математическую статистику" - 25 чел. 9 человек сдали "Теорию графов" и "Теорию вероятности", 8 человек - "Теорию графов" и "Мат. статистику", а 7 человек сдали "Теорию вероятности" и "Мат. статистику". 1 человек изучал все три дисциплины и успешно их сдал. Сколько человек не сдали экзамена ни по одной из перечисленных дисциплин?
На железнодорожной станции имеется 5 светофоров. Сколько может быть дано различных сигналов, если каждый светофор имеет 3 состояния: красный, желтый и зеленый? 
В букинистическом магазине лежат 7 экземпляров романа И.С. Тургенева "Рудин" , 2 экземпляра его же романа "Дворянское гнездо" и 3 экземпляра романа "Отцы и дети". Кроме того, есть 4 тома, содержащих романы "Рудин" и "Дворянское гнездо", и 5 томов, содержащих романы "Дворянское гнездо" и "Отцы и дети", кроме того, в магазине есть 3 тома, в которые входят "Рудин" и "Отцы и дети". Сколькими способами можно сделать покупку, содержащую по 1 экземпляру каждого из этих романов?
Сколькими способами можно составить предложение, переставляя 4 слова: "студент" "экзамен" "сдал" "хорошо"?
По результатам опроса студенческой группы из 32 человек 10 человек регулярно читает журнал "Мир ПК", 13 человек читают журнал "Открытые системы", 12 человек предпочитают журнал "Знание-сила", 5 человек читают и "Мир ПК" и "Открытые системы", 3 человека читают "Мир ПК" и "Знание-сила", 6 человек - Открытые системы" и "Знание-сила", а 1 человек читает все три журнала. Сколько человек не читает ни одного из перечисленных журналов?
Сколькими способами можно переставить буквы слова "опоссум" так , чтобы буква "п" не шла непосредственно после буквы "о"?
Даны множества 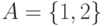 и
и 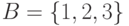 . a) записать элементы множества
. a) записать элементы множества 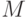 в явном виде, если
в явном виде, если 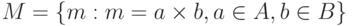 . б). записать элементы отношения
. б). записать элементы отношения 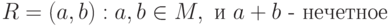 ; в). найти область определения
; в). найти область определения 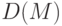 и область значений
и область значений 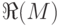 .
.
Пусть имеется множество 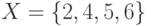 и задано отношение
и задано отношение  . Определить, какими свойствами обладает данное отношение.
. Определить, какими свойствами обладает данное отношение.
Сколько пятизначных чисел, которые одинаково читаются слева направо и справа налево (например, 67876 или 17071)?
Сколькими способами можно составить предложение, переставляя 3 слова: "кот" "сметану" "съел"?
Решение. Перестановки трех различных слов можно получить  способами, т. е. всего вариантов . . . . .
способами, т. е. всего вариантов . . . . .
Сколькими способами можно посадить за круглый стол 4 мужчин и 4 женщин так, чтобы никакие 2 лица одного пола не сидели рядом?
На железнодорожной станции имеется 4 светофора. Сколько может быть дано различных сигналов, если каждый светофор имеет 3 состояния: красный, желтый и зеленый?
В магазине имеется 80 музыкальных CD дисков и 30 дисков с фильмами. Можно купить 2 музыкальных диска или 3 диска с фильмами. В каком случае при покупке больше вариантов выбора?
По результатам опроса студенческой группы из 32 человек 12 человек регулярно читает журнал "Мир ПК", 10 человек читают журнал "Открытые системы", 8 человек предпочитают журнал "Знание-сила", 3 человека читают и "Мир ПК" и "Открытые системы", 4 человека читают "Мир ПК" и "Знание-сила", 5 человек - "Открытые системы" и "Знание-сила", а 1 человек читает все три журнала. Сколько человек не читает ни одного из перечисленных журналов?
На собрании должно выступить 7 человек: А, Б, В, Г, Д , Е и Ж. Сколькими способами можно расположить их в списке ораторов при условии, что Б не должен выступать до того, как выступит Д?
На собрании должно выступить 6 человек: А, Б, В, Г, Д и Е. Сколькими способами можно расположить их в списке ораторов при условии, что оратор А должен выступить непосредственно перед оратором Е?
В группе 22 человека. Необходимо сформировать команду из 5 человек. Сколькими способами это можно сделать?
В букинистическом магазине лежат 5 экземпляров романа И.С. Тургенева "Рудин" , 4 экземпляра его же романа "Дворянское гнездо" и 2 экземпляра романа "Отцы и дети". Кроме того, есть 5 томов, содержащих романы "Рудин" и "Отцы и дети", и 6 томов, содержащих романы "Дворянское гнездо" и "Отцы и дети". Сколькими способами можно сделать покупку, содержащую по 1 экземпляру каждого из этих романов?
На полке находятся  различных книг, из которых
различных книг, из которых  в черных переплетах, а
в черных переплетах, а  в красных. Сколько существует перестановок этих книг, при которых книги в черных переплетах занимают первые
в красных. Сколько существует перестановок этих книг, при которых книги в черных переплетах занимают первые  мест? Сколько положений, в которых все книги в черных переплетах стоят рядом?
мест? Сколько положений, в которых все книги в черных переплетах стоят рядом?
Сколькими способами можно составить трехцветный полосатый флаг, если имеется материал 6 различных цветов?
На потоке обучалось 65 студентов, все они посещали дисциплины по выбору, такие как "Теория графов", "Теория вероятности" и "Математическая статистика". Во время сессии "Теорию графов" успешно сдало 32 человека; "Теорию вероятности" - 29 человек; "Математическую статистику" - 23 чел. 8 - человек сдали "Теорию графов" и "Теорию вероятности", 7 человек - "Теорию графов" и "Мат. статистику", а 9 человек сдали "Теорию вероятности" и "Мат. статистику". 3 человека изучали все три дисциплины и успешно их сдали. Сколько человек не сдали экзамена ни по одной из перечисленных дисциплин?
Найти число целых положительных чисел, не превосходящих 200 и не делящихся ни на одно из чисел 2, 3 и 5.
К какому типу относятся следующие множества? Представить элементы множеств в явном виде, если это возможно, и подсчитать мощность множеств.
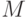 - множество цифр, например, арабских.
- множество цифр, например, арабских. - множество целых положительных четных чисел.
- множество целых положительных четных чисел. - множество двузначных чисел, являющихся степенями 2, которые нацело делятся на 5.
- множество двузначных чисел, являющихся степенями 2, которые нацело делятся на 5.

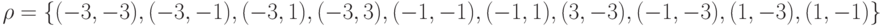 . Каким способом представлено отношение на рисунке:
. Каким способом представлено отношение на рисунке:
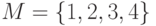 . Найти тождественное и универсальное множества.
. Найти тождественное и универсальное множества.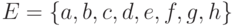 и множества
и множества  ,
,  и
и  на рисунке. Записать элементы множеств
на рисунке. Записать элементы множеств 

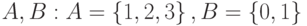 . Найти множества:
. Найти множества: 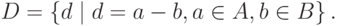
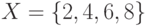 и задано отношение
и задано отношение  . Записать отношение в явном виде .
. Записать отношение в явном виде . ?
?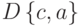 .
. . Найти множество
. Найти множество 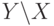
 . Найти множество и дать графическую интерпретацию операциям:
. Найти множество и дать графическую интерпретацию операциям: 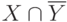
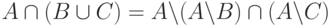 ?
?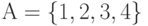 ,
, 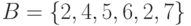 ,
, 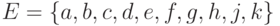 и множества
и множества 
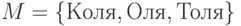 . Составить булеан множества и определить его мощность.
. Составить булеан множества и определить его мощность.

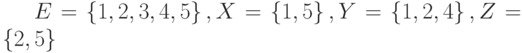 . Чему равно множество
. Чему равно множество 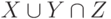




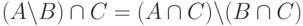 ?
? 

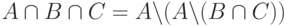 ?
? )
)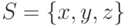 . Найти прямое произведение
. Найти прямое произведение  .
.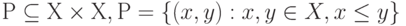 . Записать отношение в явном виде.
. Записать отношение в явном виде.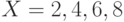 и задано отношение
и задано отношение 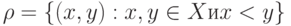 . Выписать все элементы
. Выписать все элементы 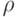 и
и 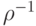 .
.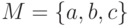 . Найти тождественное и универсальное множества.
. Найти тождественное и универсальное множества.
 . Каким способом представлено отношение на рисунке:
. Каким способом представлено отношение на рисунке:
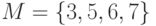 и задано отношение
и задано отношение 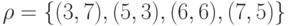 : a) является ли оно функцией? б) является ли оно отображением?
: a) является ли оно функцией? б) является ли оно отображением?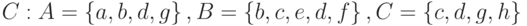 .
.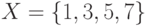 и задано отношение
и задано отношение 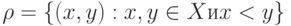 . Выписать все элементы
. Выписать все элементы 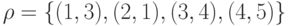 . Является ли оно функцией?
. Является ли оно функцией?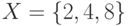 и задано отношение
и задано отношение 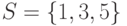 . Составить булеан множества и определить его мощность.
. Составить булеан множества и определить его мощность.
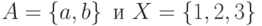 . Найти прямое произведение
. Найти прямое произведение  .
.
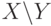
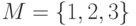 . Найти тождественное и универсальное множества.
. Найти тождественное и универсальное множества.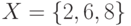 и задано отношение
и задано отношение 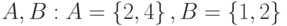 . Найти множества:
. Найти множества: 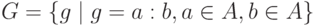
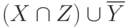
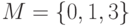 и задано отношение
и задано отношение 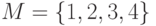 и задано отношение
и задано отношение  . Является ли оно функцией?
. Является ли оно функцией? . Найти элементы множества
. Найти элементы множества 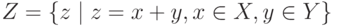 .
.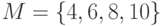 и задано отношение
и задано отношение 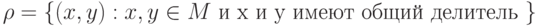 .Записать отношение в явном виде. Обладает ли данное отношение свойством эквивалентности?
.Записать отношение в явном виде. Обладает ли данное отношение свойством эквивалентности?
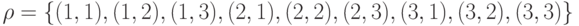 . Обладает ли данное отношение свойством эквивалентности?
. Обладает ли данное отношение свойством эквивалентности?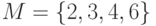 и задано отношение
и задано отношение  : a) записать отношение в явном виде; б)определить свойства отношения
: a) записать отношение в явном виде; б)определить свойства отношения 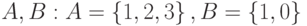 . Найти множества:
. Найти множества: 
 . Составить булеан множества и определить его мощность.
. Составить булеан множества и определить его мощность. и задано отношение
и задано отношение 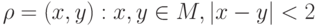 : a) записать отношение в явном виде; б) определить свойства отношения
: a) записать отношение в явном виде; б) определить свойства отношения