База ответов ИНТУИТ

Языки и исчисления - ответы

Количество вопросов - 332

Верно утверждение для произвольных литералов, конъюнктов и дизъюнктов:

Если Г - множество формул, то тогда:

Любая теория, устойчивая относительно объединения:

Процесс вывода можно представить:

Не общезначима формула:

Формулы А и В эквивалентны, если они обе:

Общезначима формула:

Предикат определяемый формулой x=const:

Для сигнатуры аксиомой равенства будет:

Если в теории Г выводима формула А \wedge \neg A(А - любая формула), то она:

Исчисление предикатов построено над:

Всякое непротиворечивое множество замкнутых формул:

Двойственна к выполнимости:

Верна формула:

Предикат "двоичное слово x входит в двоичного слова y":

Формулы класса П_1:

Для любых формул исчисления высказывания А В, С выводима формула:

При некотором C > 0 сложность большинства булевых n-местных функций:

Теоремой исчисления высказываний является:

Всякая выводимая в исчислении предикатов формула:

Теория 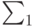\sum\nolimits_1 {} аксиоматизируема, если она:

В игре Эренфойхта игроков:

Если х - свободное вхождение в формулу А или В, то оно:

Если A и B - пропозициональные формулы, то такой же формулой будет:

Если всякое конечное подмножество теории в сигнатуре с равенством имеет нормальную модель, то теория:

Для умножения двух n-разрядных двоичных чисел существует схема:

Тавтологией является формула (A, B - формулы):

Если все П1-формулы сигнатуры S с равенством, выводимые из теории Т, истинны в А, то:

Любые два алгебраически замкнутых поля конечной характеристики n:

Аксиомой исчисления высказываний является:

Если A и B - пропозициональные формулы, то такой же формулой будет:

Тавтологией является формула (A,B - формулы):

Тавтологией является формула (A,B - формулы):

Верно утверждение для любой булевой функции f от n аргументов:

Верна теорема для любой булевой функции f:

Функция f = x \wedge \overline {x \wedge y \vee x} эквивалентна:

В списке выражений: 2-2=0, 2+3=6, 3+12, 2+2>2+2, 2-0=3-0, 56=50+6 приведено всего истинных и ложных высказываний соответственно:

Схема "ИЛИ - НЕ" имеет:

Полным набором B булевых функций называется набор, для которого:

Сложность большинства булевой n-местной функций при наибольшем размере C их схем:

Если B - полный базис, то существует 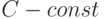C - const:

Если 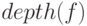depth(f) - минимальная глубина схемы, вычисляющая функцию f, то:

Отношение x>y (x, y - натуральные) является:

Аксиомой исчисления высказываний является:

Аксиомой исчисления высказываний является:

Выводом является:

Любая тавтология в исчислении высказываний есть:

Если А, В, С - формулы, то:

Теоремой исчисления высказываний является:

Для произвольных формул А, В:

Поиск контрпримера для формулы А сводится к поиску:

Контрпример к секвенции 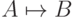A \mapsto B - это набор значений переменных, для которых все формулы:

Верно правило для некоторых конечных множеств формул А, В, С, Д:

Правило вывода в исчислении секвенций - это правило, объявляющее:

Секвенция выводима тогда и только тогда, когда она:

В выводе секвенции принципиально новое, не содержащегося в секвенции всегда:

Верна формула:

Если М - непустое множество, то множество всех <m1, m2,…, mk> - это:

Бинарным предикатом на множестве М будет:

Количество различных 1-местных предикатов:

Если А - предикатный символ валентности k, t1, t2, …, tk - термы, то выражение А(t1, t2, …, tk) - это:

Формулу можно построить с использованием правила:

Если А - формула, а x - ее индивидная переменная, то:

Чтобы задать интерпретацию сигнатуры S, необходимо:

Параметром формулы A может быть:

Арифметическое множество - это множество:

Предикат определяемый формулой 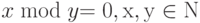x\bmod y{\rm = 0}{\rm , x}{\rm , y} \in {\rm N}:

Предикат определяемый формулой 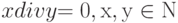x{\rm }div{\rm }y{\rm = 0}{\rm , x}{\rm , y} \in {\rm N}:

Предикат "z=x+y", где "+" - конкатенация двоичных слов:

Предикат "двоичное слово x - конец двоичного слова y":

Предикат "x=2n", n - натуральное:

Биекция 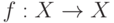f:X \to X - автоморфизм интерпретации, если все функции и предикаты интерпретации:

Класс выразимых предикатов:

В 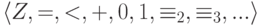\left\langle {Z, = , < , + ,0,1, \equiv _2 , \equiv _3 ,...} \right\rangle элиминация кванторов:

Бескванторная формула сигнатуры 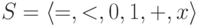S = \left\langle { = , < ,0,1, + ,x} \right\rangle :

Для семейства многочленов Pn(x), отбрасывание старшего члена:

Для семейства многочленов Pn(x), взятие старшего коэффициента:

Две интерпретации - изоморфны, если между ними существует:

Композиция двух изоморфизмов:

Естественные интерпретации сигнатуры S = \left\langle { = , < , + ,0,1} \right\rangle на носителе R:

Если группа - интерпретация сигнатуры 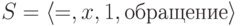S = \left\langle { = ,x,1,обращение} \right\rangle , то подструктуры - это:

Игра Эренфойхта определяется:

В игре Эренфойхта:

У Консерватора есть способ выиграть если интерпретации:

Для упорядоченных множеств сигнатуры 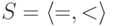S = \left\langle { = , < } \right\rangle и носителей Z и Q:

Глубина атомарных формул равна:

Глубина формулы 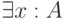\exists x:A:

Две формулы с параметрами эквивалентны, если они одновременно:

Для счетного (конечного) подмножество интерпретации M:

Формулы А и В эквивалентны, если формула:

Формула, истинная в некоторой интерпретации на некоторой оценке называется:

Если х - свободное вхождение в формулу А, то оно всегда:

Если х - свободное вхождение в формулу А или В, то оно:

Если выводима формула А(с/х), где А - формула, х - переменная, с - константа не входящая в А, то тогда:

Теория Г в сигнатуре S - это произвольное:

Теория Г противоречива, если в ней выводима

Непротиворечиво:

Любое совместное множество замкнутых формул:

Если А - замкнутая формула сигнатуры непротиворечивого множества Г и выводима А, то:

Множество всех истинных в N формул сигнатуры 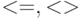< =, < > не выводится формула:

Замкнутым термам соответствуют:

Если 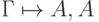Г \mapsto A, A - формула, Г - непротиворечива, то:

Если прототип формулы - тавтология, то бескванторная формула:

Значения разных атомарных формул выбирать независимо:

Формула 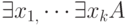\exists x_{1,} \cdots \exists x_k A (А - бескванторная ) общезначима, если общезначима дизъюнкция подстановок:

Теорема Эрбрана:

Для замкнутой А можно указать B \in П_1 этой же сигнатуры с добавленными функциональными символами, которая:

"Сколемовская нормальная форма" позволяет получать формулы класса:

Вопрос о выводимости формулы исчисления предикатов сводится к выводимости:

Алгоритм, который по произвольной замкнутой формуле определяет ее выводимость:

Для сигнатуры аксиомой равенства будет:

Теория сигнатуры с равенством имеет нормальную модель тогда и только тогда, когда:

Если А - бесконечная нормальная интерпретация сигнатуры S с равенством m \ge \left| s \right|,m \ge \left| A \right|, то нормальное элементарное расширение мощности m:

Семантическое следование равносильно:

Непротиворечивая теория с равенством в не более счетной сигнатуре, не имеющая конечных моделей и категоричная в несчетной мощности:

В теорию плотных линейных упорядоченных множеств без первого и последнего элемента входит аксиома:

В теорию плотных линейных упорядоченных множеств без первого и последнего элемента входит аксиома:

Арифметика Пеано - это арифметика:

Истинность бескванторных формул из D(A) от присутствия дополнительных элементов:

Нормальная интерпретация А сигнатуры S с равенством может быть расширена до нормальной модели теории Т, если:

Если T1, T2 - теории сигнатуры с равенством, то:

Теория Т - П1 аксиоматизируема, если существуют П1-формулы,из которых:

Чтобы задать подструктуру нормальной интерпретации В, нужно взять подмножество носителя В:

Если любая подструктура любой нормальной модели является ее моделью, то теория:

Если любая подструктура любой нормальной модели является ее моделью, то теория:

Если S не пусто, F \in 2^S , то для того, чтобы F был фильтром нужно:

Если S не пусто, F \in 2^S , то для того, чтобы F был фильтром нужно:

Любой главный фильтр является:

Свойство ультрафильтра отражает:

Ультрапроизведение семейства моделей некоторой теории моделью той же теории:

Среди гипердействительных чисел есть:

Нестандартные гипернатуральные числа:

Если существует бесконечно далекий ak из ряда ‹ai›, I=0,1,… который бесконечно близок к а, то:

Голосование можно проводить для:

Верно утверждение для произвольных литералов, конъюнктов и дизъюнктов:

Любое вхождение переменной в терм:

Конструктивно определяемая последовательность переменных, занятых, скобок и символов сигнатуры называется:

Общезначима формула:

Для любой формулы А, формула А →​ А есть:

Чтобы задать интерпретацию сигнатуры S, необходимо:

Всякий фильтр F на S расширить до ультрафильтра G \supset F:

Арифметические формулы определяются сигнатурой S, носителем N вида:

Теорема о полноте позволяет заменить в формулировке:

Функция f = x \wedge \overline { x \wedge y \vee x \wedge \overline y } эквивалентна:

Верна формула:

Для произвольных формул А, В:

Глубина формулы 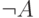\neg A равна:

Верно утверждение:

Если в Г все формулы истинны в интерпретации М, то для некоторой замкнутой формулы А:

Замкнутая формула невыполнима, если:

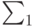\sum\nolimits_1 {} - теорема \exists x_1 ...\exists x_2 А теории T1 и отрицающая ее П1-теорема \forall x_1 ...\forall x_n А теории T2:

В теории действительных чисел со сложением и умножением, элиминация кванторов:

Без аксиомы "исключенного третьего" выводима:

Из выводимости "Сколемовской нормальной формы", выводимость формулы:

Контрпример к секвенции 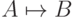A \mapsto B будет контрпримером к формуле ( 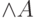\wedge A - конъюнкция, 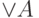\vee A - дизъюнкция формул из А)

Верно правило для некоторых конечных множеств формул А, В, С, Д:

Если А - бесконечная нормальная интерпретация сигнатуры с равенством,то нормальная интерпретация В А большой мощности , является элементарным расширением А:

Общезначима формула:

В противоречивой теории:

Непротиворечивая теория с равенством в не более счетной сигнатуре, не имеющая конечных моделей и категоричная в счетной мощности:

Количество всех n-местных булевых функций равно:

Формулу можно построить с использованием правила:

Набор символов-обозначений в формулах с неотрицательными числами называется:

Если теория П1 аксиоматизируема, то подструктура ее нормальной модели является:

Алгоритм вывода формул 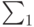\sum _1:

Верна теорема для любой булевой функции f:

Сложность булевой функции относительно базисных функций - это:

Количество всех различных n-местных схем размера m оценивается:

Для сложения двух n-разрядных двоичных чисел:

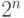Вычитание двух n-разрядных двоичных чисел по модулю 2^n выполнима схема:

Для вычисления функции голосования существует схема:

Отношение x mod y=0 (x, y - натуральные) является:

Аксиомой исчисления высказываний является:

Аксиомой исчисления высказываний является:

Выводом является:

Если Г - множество формул, то:

Если А, В, С - формулы, то:

Исчисление секвенций - исчисление типа:

Интуиционистское исчисление высказываний получается:

Верна формула:

Без аксиомы "исключенного третьего" выводима:

Количество синонимов в списке ‹"арность", "местность", "валентность", "эквивалентность"› равна:

Количество различных 0-местных предикатов равно:

Предикат "\neg \exists {\rm }y \ne 1,x:x{\rm }\bmod {\rm }y = 0,{\rm }x,y \in N":

Предикат "двоичное слово x состоит только из нулей":

Бескванторная формула сигнатуры 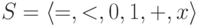S = \left\langle { = , < ,0,1, + ,x} \right\rangle :

Для всякой формулы F сигнатуры 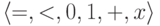\left\langle { = , < ,0,1, + ,x} \right\rangle существует бескванторная формула, задающая F на R - это:

Для сигнатуры 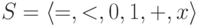S = \left\langle { = , < ,0,1, + ,x} \right\rangle и носителя С (комплексные числа) всякая формула:

Для некоторой сигнатуры S две ее интерпретации называются элементарно эквивалентными, если:

Тождественное отображение:

Минимальное число слагаемых в сумме вида 1+1+…+1, при котором она обращается в нуль - это:

В игре Эренфойхта игроки:

Для упорядоченных множеств сигнатуры 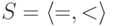S = \left\langle { = , < } \right\rangle и носителей N и Z:

Для упорядоченных множеств сигнатуры 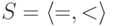S = \left\langle { = , < } \right\rangle и носителей R и Q:

Для счетной (конечной) сигнатуры и бесконечной ее интерпретации M:

Формула, истинная в любой интерпретации сигнатуры называется:

Не общезначима формула:

Формулы А и В эквивалентны, если формула:

Любое вхождение переменной в атомарную формулу:

Если х - свободное вхождение в формулу А или В, то оно:

Теория Г может быть:

Множество Г с моделью называется:

Из множества всех истинных в N формул сигнатуры 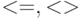< =, < > не выводится формула:

Любая непротиворечивая теория:

Бескванторная формула выводима, если ее прототип является:

Из выводимости формулы, выводимость ее "Сколемовской нормальной формы":

Однородное линейное упорядоченное множество такой же мощности для всякой бесконечной мощности:

В теорию плотных линейных упорядоченных множеств без первого и последнего элемента входит аксиома:

В теорию плотных линейных упорядоченных множеств без первого и последнего элемента входит аксиома:

Сигнатура теории полугрупп состоит из:

Если T1, T2 - теории сигнатуры с равенством, то:

Если теория устойчива относительно перехода к подструктурам, то она:

Если S не пусто, F \in 2^S , то для того, чтобы F был фильтром нужно:

Если S не пусто, F \in 2^S , то для того, чтобы F был фильтром нужно:

Все нестандартные гипернатуральные числа:

Если все элемнеты гипердействительного аналога множества M \subset R конечны, то:

n - местный предикат P - устойчив относительно автоморфизма 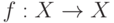f:X \to X, если:

Всякая формула в 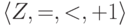\left\langle {Z, = , < , + 1} \right\rangle , где +1 - функция прибавления 1:

Предикат "двоичные слова x и y имеют одинаковую длину":

Схема "И - НЕ" имеет:

В игре Эренфойхта, если есть предикат сигнатуры, различающий помеченные элементы интерпретации, то:

Из множества всех истинных в N формул сигнатуры 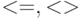< =, < > не выводится формула:

Верно правило для некоторых конечных множеств формул А, В, С, Д:

Предикат "двоичное слово x - начало двоичного слова y":

Формулу можно построить с использованием правила:

Формула А семантически следует из теории T,если она:

Число возможных диаграмм семейства многочленов:

Теория Г может быть:

Тавтологией является формула (A,B - формулы):

Сложность любой булевой n-местной функций при наибольшем размере C их схем:

Для сложения двух n-разрядных двоичных чисел:

Аксиомой исчисления высказываний является:

Теоремой исчисления высказываний является:

Формула, представляющая секвенцию 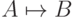A \mapsto B:

Формулу можно построить с использованием правила:

Параметром формулы A может быть:

Предикат определяемый формулой x \le y,{\rm }x,y \in N:

Предикат "x=4n", n - натуральное:

Выразимые в арифметике Пресбургера предикаты - это бескванторные формулы из:

Отображение, обратное изоморфизму будет:

Игроки игры Эренфойхта называются:

Глубина формулы 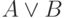A \vee B равна:

Если бесконечное множество противоречиво, то некоторое его конечное подмножество будет:

Если в Г все формулы истинны в интерпретации М, то для некоторой замкнутой формулы А:

Если А - замкнутая формула сигнатуры непротиворечивого множества Г и выводима 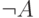\neg A, то:

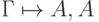Если Г \mapsto A, A - формула, Г - непротиворечива, то:

Общезначимость формулы 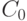C_0 свободными переменными равносильна общезначимости ее:

Если существуют подстановки A(y_1 /x_1 \ldots y{}_k/x_k ), \ldots ,A(w_1 /x_1 \ldots w_k /x_k ) для которых общезначима дизъюнкция, то формула \exists x_1 \ldots \exists x_k A(А - бескванторна):

Утверждение 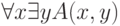\forall x\exists y{\rm }A(x,y) нельзя записать в виде:

Если отрицание замкнутой формулы общезначимо, то она:

Конечно аксиоматизируемая полная теория в конечной сигнатуре:

В теорию плотных линейных упорядоченных множеств без первого и последнего элемента входит аксиома:

Любую модель теории D(A) можно считать расширением интерпретации А, если:

Ультрафильтр - это фильтр:

Аксиомы равенства в фильтрованном произведении нормальных интерпретаций:

Если А и В - некоторые конечные множества формул, то секвенция обозначается:

Если теория имеет сколь угодно большое конечные нормальные модели, то она:

Все теоремы теории Г:

Для вычисления функции голосования существует схема:

Отметьте высказывание, которое является выражением:

Если всякий многочлен Pn(x),n>0 имеет в поле X хотя бы один корень, то:

Верна теорема для любой булевой функции f:

Унарным предикатом на множестве М будет:

Тавтологией является формула (A,B - формулы):

Функция 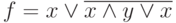f = x \vee \overline {x \wedge y \vee x} эквивалентна:

Если A и B - полные наборы булевых функций, то для любой функции:

Если А, В, С - формулы, то:

Интуиционистская логика возникла как попытка формализовать:

Параметром формулы A может быть:

Множество натуральных чисел, не являющееся арифметическим:

Предикат z=НОД(x,y), x,y \in N:

Предикат "x - простое число номер n":

Предикат "x>y", x,y - целое:

Для упорядоченных множеств сигнатуры 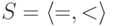S = \left\langle { = , < } \right\rangle и носителей Z и R:

Итерации A и B элементарно эквивалентны тогда и только тогда, когда в соответствующей игре Эренфойхта:

Если в бескванторной формуле заменить атомы на пропозициональные, то получим формулу:

Формула \exists x_1 \ldots \exists x_k A, c,d - const:

Утверждение 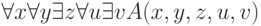\forall x\forall y\exists z\forall u\exists vA(x,y,z,u,v) выполнимо только тогда, когда выполнимо:

Множество теорем теории равенств:

Кольцо может быть в поле, если:

Если T1, T2 - теории сигнатуры с равенством, то:

Теория П1 аксиоматизируема, если она:

Теория Т - 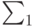\sum\nolimits_1 {} аксиоматизируема, если существуют 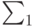\sum\nolimits_1 {} -формулы, из которых:

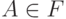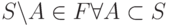Фильтр на S со свойством A \in F или S\backslash A \in F\forall A \subset S называется:

Если ультрафильтр неглавный, то:

Всякое конечное гипердействительное число бесконечно близко к:

Для произвольных формул А, В:

Для умножения двух n-разрядных двоичных чисел существует схема:

Любые два плотно упорядоченных множества без первого и последнего элемента:

Вопрос о выводимости произвольных формул языка первого порядка:

Чтобы задать интерпретацию сигнатуры S, необходимо:

Глубина формулы A \wedge B равна:

Если A и B - пропозициональные формулы, то такой же формулой будет:

k-местной функцией на М является:

Тернарным (тренарным) предикатом на множестве М будет:

Формулу можно построить с использованием правила:

Предикат, выразимый в данной интерпретации:

Для семейства многочленов Pn(x), дифференцирование по X:

Любые два алгебраически замкнутых поля характеристики О:

Число ходов Новатора соответствует:

Если в тавтологию вместо пропозициональных переменных подставить формулы сигнатуры, получим:

Общезначима формула:

Вхождение индивидной переменной, не из области действия одноименного квантора называется:

Теория Г противоречива, если в ней выводится:

Алгоритм вывода формул 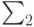\sum _2:

Множество истинных бескванторных формул сигнатуры с равенством и константами для всех элементов интерпретации - это:

Если теория 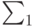\sum\nolimits_1 {} аксиоматизируема, то подструктура ее нормальной модели является:

Любая теория, имеющая П2-аксиоматизацию:

Если S не пусто, F \in 2^S , то для того, чтобы F был фильтром нужно:

Среди гипердействительных чисел есть:

Число а - предел ‹ai›, i=0,1,…, если есть бесконечно далекий ak:

Если S не пусто, F \in 2^S , то для того, чтобы F был фильтром нужно:

Схема "ИСКЛЮЧАЮЩЕЕ - ИЛИ" имеет:

Размером схемы называется число:

Всякая коммутативная полугруппа с сокращением:

Множество 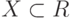X \subset R ограничено, если все элементы его гипердействительного аналога:

Формулы A и B эквивалентны тогда и только тогда, когда тавтологией является формула:

Отношение x + 5=y (x, y - натуральные) является:

Выводом является:

Количество 2-местных предикатов:

В игре Эренфойхта:

Интерпретация М теории Г, в которой все формулы из Г истинны в М - это:

Если теория устойчива относительно перехода к подструктурам, то она:

Глубина формулы 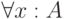\forall x:A:

Если удалить символ < из сигнатуры 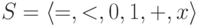S = \left\langle { = , < ,0,1, + ,x} \right\rangle , класс выразимых предикатов:

Секвенция, в обеих частях которой встречаются только переменные, причем хоть одна из них встречается в обеих частях - это:

Для сигнатуры аксиомой равенства будет:

В теорию плотных линейных упорядоченных множеств без первого и последнего элемента входит аксиома:

Вариант исчисления высказываний - исчисление:

Для любого непротиворечивого множества замкнутых формул полное непротиворечивое множество замкнутых формул той же сигнатуры:

Если секвенция выводима в исчислении секвенций, то представляющая ее формула в исчислении высказываний:

Если Г - множество формул, то: