Математический анализ. Интегрирование - ответы
Количество вопросов - 220
Функция  - интегрируема по Риману на
- интегрируема по Риману на ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) . Тогда предел интегральных сумм этой функции
. Тогда предел интегральных сумм этой функции
Площадь криволинейной трапеции, заданной параметрически 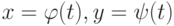 , вычисляется по формуле:
, вычисляется по формуле:
Дифференциал  длины дуги кривой
длины дуги кривой 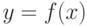 вычисляется по формуле
вычисляется по формуле
Пусть задан интеграл 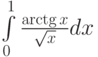 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Пусть 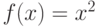 и
и 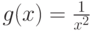 . Отметьте интегрируемые функции на отрезке
. Отметьте интегрируемые функции на отрезке ![[0,1]](https://intuit.ru//sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) :
:
Пусть задана функция 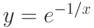 . Тогда она интегрируема на отрезке
. Тогда она интегрируема на отрезке
Несобственный интеграл 1 рода сходится, если предел функции 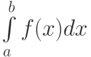 при
при 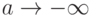
Пусть площадь фигуры, заключённой между кривыми  вычисляется по формуле
вычисляется по формуле ![\int\limits_a^b[f(x)-g(x)]dx](https://intuit.ru//sites/default/files/tex_cache/57673ffb275d75cc9b911691b8b77aa5.png) . Какие условия должны выполняться:
. Какие условия должны выполняться:
Отметьте верные утверждения:
Число 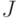 называется пределом интегральных сумм
называется пределом интегральных сумм  функции
функции  на
на ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) , если
, если 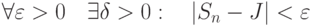
Объём тела вращения вычисляется по формуле:
На каком отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) для вычисления интеграла
для вычисления интеграла 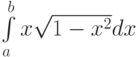 можно применить подстановку
можно применить подстановку 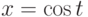 :
:
Объём тела вращения дуги параболы 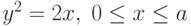 вычисляется по формуле:
вычисляется по формуле:
Масса неоднородного стержня плотности 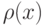 на отрезке
на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) равна
равна 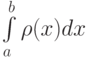 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Длина 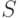 кривой
кривой 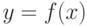 в прямоугольных координатах вычисляется по формуле
в прямоугольных координатах вычисляется по формуле
Рассмотрим несобственные интегралы 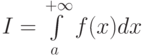 и
и 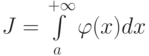 для функций, связанных неравенством
для функций, связанных неравенством 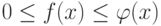 . Отметьте верные утверждения:
. Отметьте верные утверждения:
При каких условиях справедлива формула 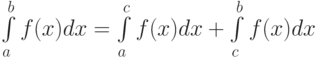
Отметьте верные утверждения:
Площадь фигуры, ограниченной кривой  , вычисляется по формуле:
, вычисляется по формуле:
Пусть задан несобственный интеграл 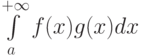 .Признак Абеля-Дирихле является для интеграла критерием :
.Признак Абеля-Дирихле является для интеграла критерием :
Кривая 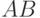 называется спрямляемой, если предел длины
называется спрямляемой, если предел длины  вписанной ломаной при
вписанной ломаной при 
Пусть задан интеграл  . Отметьте верные утверждения:
. Отметьте верные утверждения:
Для несобственного интеграла 1 рода 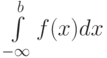 функция
функция  :
:
Рассмотрим несобственный интеграл 1 рода 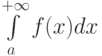 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Интегралом с переменным верхним пределом называется функция 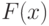 , равная
, равная
Пусть 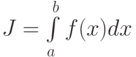 - определённый интеграл функции
- определённый интеграл функции  на
на ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) . Тогда
. Тогда
В каких случаях разность двух функций  всегда интегрируемая:
всегда интегрируемая:
Пусть 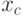 - координата центра тяжести неоднородного стержня плотности
- координата центра тяжести неоднородного стержня плотности 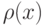 на отрезке
на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) . Тогда она равна отношению к массе стержня
. Тогда она равна отношению к массе стержня
Рассмотрим несобственный интеграл 1 рода 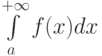 от неотрицательной функции. Отметьте верное утверждение:
от неотрицательной функции. Отметьте верное утверждение:
Рассмотрим несобственный интеграл 2 рода 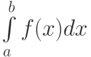 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Какой должна быть функция сравнения 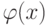 при исследовании на сходимость интеграла
при исследовании на сходимость интеграла 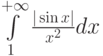 :
:
Пусть 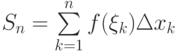 - интегральная сумма функции
- интегральная сумма функции  на
на ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) . Тогда
. Тогда
Пусть 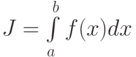 - определённый интеграл функции
- определённый интеграл функции  на
на ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) . Тогда
. Тогда
Отметьте верное утверждение:
Пусть задана функция 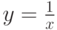 . Тогда она интегрируема на отрезке
. Тогда она интегрируема на отрезке
Пусть задана функция 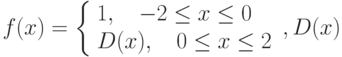 - функция Дирихле. Тогда функция
- функция Дирихле. Тогда функция  интегрируема на отрезке
интегрируема на отрезке
Отметьте верные равенства:
В каких случаях разность двух функций  может быть интегрируемая:
может быть интегрируемая:
Пусть 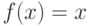 и
и  . Отметьте интегрируемые функции на отрезке
. Отметьте интегрируемые функции на отрезке ![[0,1]](https://intuit.ru//sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) :
:
Пусть функция  интегрируема на отрезке
интегрируема на отрезке ![[a,c]](https://intuit.ru//sites/default/files/tex_cache/209f61583177d88b1f24c85f6a43c6ff.png) и интегрируема на отрезке
и интегрируема на отрезке ![[c,b]](https://intuit.ru//sites/default/files/tex_cache/d6033df87877013a91e322ce6a5bc181.png) . Тогда она на отрезке
. Тогда она на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png)
При каких условиях справедлива формула 
Пусть  . Для каких отрезков
. Для каких отрезков 
При выполнении условий теоремы о среднем
Среднее значение функции на отрезке является одним из значений функции на этом отрезке, если функция на отрезке
Для каких подынтегральных функций  интеграл с переменным верхним пределом является первообразной:
интеграл с переменным верхним пределом является первообразной:
Пусть задана функция 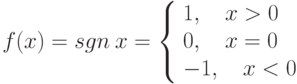 . Тогда эта функция на отрезке
. Тогда эта функция на отрезке ![[-1,1]](https://intuit.ru//sites/default/files/tex_cache/d060b17b29e0dae91a1cac23ea62281a.png)
Производная интеграла с переменным верхним пределом равна
Производная интеграла с переменным нижним пределом равна
Пусть функция  непрерывна на отрезке
непрерывна на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) . Тогда она на этом отрезке
. Тогда она на этом отрезке
Пусть функция  непрерывна на отрезке
непрерывна на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) ,
, 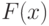 - её первообразная. Тогда
- её первообразная. Тогда 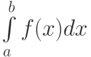 равен
равен
При вычислении каких интегралов применима формула Ньютона-Лейбница:
Найдите производные 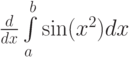 ,
, 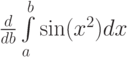 ,
, 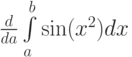 , соответственно:
, соответственно:
Какая формула при выполнении необходимых условий для функций 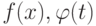 (непрерывности, дифференцируемости, значений на концах отрезка и др.) справедлива:
(непрерывности, дифференцируемости, значений на концах отрезка и др.) справедлива:
Отметьте условия, при которых справедлива формула замены переменных 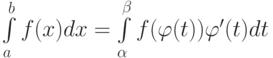
Какой новый отрезок интегрирования ![[\alpha,\beta]](https://intuit.ru//sites/default/files/tex_cache/76ec9b92b11ea1475095ec6a47fccd53.png) можно взять для вычисления интеграла
можно взять для вычисления интеграла 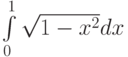 с помощью замены
с помощью замены 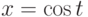 :
:
Пусть  - нечётная функция, интегрируемая на отрезке
- нечётная функция, интегрируемая на отрезке ![[-\alpha,\alpha]](https://intuit.ru//sites/default/files/tex_cache/a1dc819aa90198e790a2b8588824c63f.png) . Тогда
. Тогда 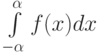 равен
равен
Какую подстановку можно использовать при вычислении интеграла 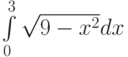 :
:
Отметьте условия, при которых справедлива формула интегрирования по частям 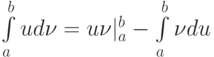 :
:
Площадь криволинейной трапеции для непрерывной и знакопеременной функции  на
на ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) :
: 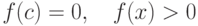 для
для  и
и  для
для ![x\in(c,b]](https://intuit.ru//sites/default/files/tex_cache/168d1fec2c62ca23128936b96a6348ca.png) равна
равна
Площадь фигуры, ограниченной линиями 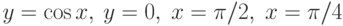 вычисляется по формуле
вычисляется по формуле
Пусть площадь фигуры, заключённой между кривыми  вычисляется по формуле
вычисляется по формуле ![\int\limits_a^b[f(x)-g(x)]dx](https://intuit.ru//sites/default/files/tex_cache/57673ffb275d75cc9b911691b8b77aa5.png) . Какие условия должны выполняться:
. Какие условия должны выполняться:
Площадь фигуры, ограниченной кривыми 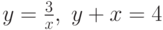 , вычисляется по формуле
, вычисляется по формуле
Площадь, ограниченная кривой 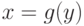 и осью ординат, вычисляется по формуле:
и осью ординат, вычисляется по формуле:
Площадь криволинейного сектора 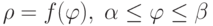 вычисляется по формуле
вычисляется по формуле 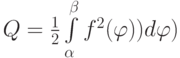 . Тогда
. Тогда
Площадь фигуры, ограниченной кривой 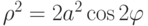 , вычисляется по формуле:
, вычисляется по формуле:
Площадь сечения 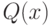 тела плоскостью, перпендикулярной к оси
тела плоскостью, перпендикулярной к оси  ,-
,-
Объем тела с известными поперечными сечениями 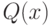 вычисляется по формуле
вычисляется по формуле  . Тогда
. Тогда
Объём тела с известными поперечными сечениями вычисляется по формуле:
Объём тела вращения эллипса  вокруг оси
вокруг оси  вычисляется по формуле:
вычисляется по формуле:
Длиной 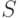 кривой
кривой 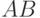 называется
называется
Длина 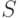 кривой, заданной в параметрической форме уравнениями
кривой, заданной в параметрической форме уравнениями 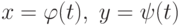 , вычисляется по формуле
, вычисляется по формуле
При вычислении длины кривой в полярных координатах функция 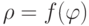 на отрезке
на отрезке ![[\alpha,\beta]](https://intuit.ru//sites/default/files/tex_cache/76ec9b92b11ea1475095ec6a47fccd53.png) должна удовлетворять условиям:
должна удовлетворять условиям:
Длина кривой в прямоугольных координатах вычисляется по формуле ![\int\limits_a^b\sqrt{1+[f'(x)]^2}dx](https://intuit.ru//sites/default/files/tex_cache/32cff20a8f8fa48bc06e3ff8d1633301.png) . Отметьте верные утверждения:
. Отметьте верные утверждения:
Длина цепной линии 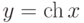 на отрезке
на отрезке ![[0,a]](https://intuit.ru//sites/default/files/tex_cache/13596d6674a86fdafa24c4c414033e58.png) вычисляется по формуле:
вычисляется по формуле:
Пусть  - масса неоднородного стержня на отрезке
- масса неоднородного стержня на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) плотности
плотности 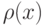 . Тогда она равна
. Тогда она равна
При вычислении работы  переменной силы функция
переменной силы функция  на отрезке
на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) должна быть:
должна быть:
Масса неоднородного стержня плотности 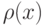 на отрезке
на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) вычисляется по формуле
вычисляется по формуле
Работа переменной силы  на отрезке
на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) равна
равна  . Отметьте верные утверждения:
. Отметьте верные утверждения:
При вычислении определённого интеграла 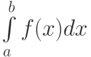 методом парабол точки разбиения кривой
методом парабол точки разбиения кривой 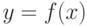 соединены
соединены
Отметьте верные утверждения:
Рассмотрим интеграл  . Отметьте верные утверждения:
. Отметьте верные утверждения:
Какой должна быть функция сравнения 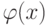 при исследовании на сходимость интеграла
при исследовании на сходимость интеграла 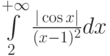 :
:
Рассмотрим несобственные интегралы 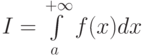 и
и 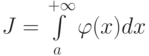 от неотрицательных функций, для которых существует конечный предел
от неотрицательных функций, для которых существует конечный предел 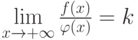 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Какой должна быть функция сравнения 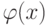 при исследовании на сходимость интеграла
при исследовании на сходимость интеграла ![\int\limits_1^{+\infty}\frac{dx}{\sqrt[3]{x^2+1}}dx](https://intuit.ru//sites/default/files/tex_cache/b6955af06658f2c5946a80d36bfcb4ff.png) :
:
Рассмотрим несобственный интеграл 1 рода 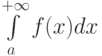 от неотрицательной функции. Отметьте верные утверждения:
от неотрицательной функции. Отметьте верные утверждения:
Интеграл 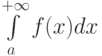 условно сходится. Отметьте верные утверждения:
условно сходится. Отметьте верные утверждения:
Отметьте верные утверждения:
Рассмотрим несобственный интеграл 1 рода 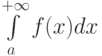 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Какую функцию сравнения 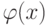 можно рассмотреть для доказательства абсолютной сходимости интеграла
можно рассмотреть для доказательства абсолютной сходимости интеграла 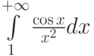 :
:
Пусть интеграл 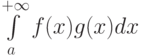 сходится. Отметьте верные утверждения:
сходится. Отметьте верные утверждения:
Пусть задан интеграл 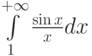 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Отметьте верные утверждения:
Пусть задан интеграл 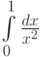 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Рассмотрим несобственные интегралы 2 рода 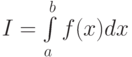 и
и  для функций, связанных неравенством
для функций, связанных неравенством 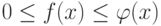 на
на 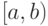 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Рассмотрим несобственные интегралы 2 рода 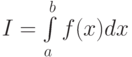 и
и  от неотрицательных на
от неотрицательных на 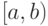 функций, для которых существует конечный предел
функций, для которых существует конечный предел 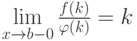 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Рассмотрим несобственный интеграл 2 рода 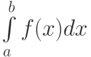 . Отметьте верные утверждения:
. Отметьте верные утверждения:
При вычислении  - массы неоднородного стержня на отрезке
- массы неоднородного стержня на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) функция
функция 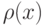 должна быть:
должна быть:
Площадь, ограниченная кривой 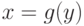 и осью ординат, вычисляется по формуле
и осью ординат, вычисляется по формуле 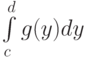 . Пределы интегрирования
. Пределы интегрирования  - это:
- это:
Пусть 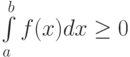 . Тогда для любого
. Тогда для любого ![x\in[a,b]](https://intuit.ru//sites/default/files/tex_cache/c7c42309c359c25dfe77f397d5261997.png)
Пусть 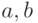 - корни уравнения
- корни уравнения  и
и 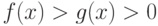 для любого
для любого 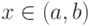 . Тогда площадь фигуры между этими кривыми вычисляется по формуле:
. Тогда площадь фигуры между этими кривыми вычисляется по формуле:
Пусть функция  непрерывна на отрезке
непрерывна на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) . Тогда
. Тогда 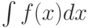
Число 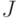 называется пределом интегральных сумм
называется пределом интегральных сумм  функции
функции  на
на ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) , если
, если  для любого разбиения
для любого разбиения ![[a,b]:\Delta x_k<\delta](https://intuit.ru//sites/default/files/tex_cache/c411055598b353d591251014a426935c.png)
На каком отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) для вычисления интеграла
для вычисления интеграла 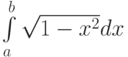 можно применить подстановку
можно применить подстановку  :
:
Пусть 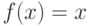 и
и 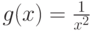 . Отметьте интегрируемые функции на отрезке
. Отметьте интегрируемые функции на отрезке ![[0,1]](https://intuit.ru//sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) :
:
Несобственный интеграл 2 рода сходится, если предел функции 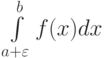 при
при 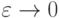
Пусть 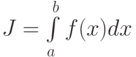 - определённый интеграл функции
- определённый интеграл функции  на
на ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) . Тогда
. Тогда
При вычислении каких интегралов применима формула Ньютона-Лейбница:
Производная интеграла с переменным нижним пределом равна подынтегральной функции со знаком минус в
Площадь фигуры, ограниченной кривыми 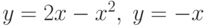 , вычисляется по формуле
, вычисляется по формуле
Длина кривой, заданной параметрически, вычисляется по формуле  . Отметьте верные утверждения:
. Отметьте верные утверждения:
Пусть задана функция 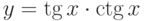 . Тогда она интегрируема на отрезке
. Тогда она интегрируема на отрезке
Какую подстановку можно использовать при вычислении интеграла 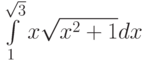 :
:
При вычислении определённого интеграла 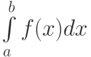 методом трапеций точки разбиения кривой
методом трапеций точки разбиения кривой 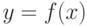 соединены
соединены
Площадь фигуры, ограниченной кривой  , вычисляется по формуле:
, вычисляется по формуле:
Площадь криволинейного сектора 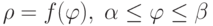 вычисляется по формуле
вычисляется по формуле 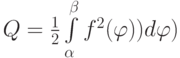 . Тогда
. Тогда
Пусть  - чётная функция, интегрируемая на отрезке
- чётная функция, интегрируемая на отрезке ![[-\alpha,\alpha]](https://intuit.ru//sites/default/files/tex_cache/a1dc819aa90198e790a2b8588824c63f.png) . Тогда
. Тогда 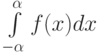 равен
равен
При вычислении 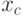 - координаты центра тяжести неоднородного стержня на отрезке
- координаты центра тяжести неоднородного стержня на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) функция
функция 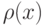 должна быть:
должна быть:
Пусть  .Тогда для любого
.Тогда для любого ![x\in[a,b]](https://intuit.ru//sites/default/files/tex_cache/c7c42309c359c25dfe77f397d5261997.png)
Какой новый отрезок интегрирования ![[\alpha,\beta]](https://intuit.ru//sites/default/files/tex_cache/76ec9b92b11ea1475095ec6a47fccd53.png) можно взять для вычисления интеграла
можно взять для вычисления интеграла 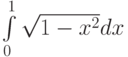 с помощью замены
с помощью замены  :
:
Пусть функция  интегрируема на отрезке
интегрируема на отрезке ![[a,c]](https://intuit.ru//sites/default/files/tex_cache/209f61583177d88b1f24c85f6a43c6ff.png) , но не интегрируема на отрезке
, но не интегрируема на отрезке ![[c,b]](https://intuit.ru//sites/default/files/tex_cache/d6033df87877013a91e322ce6a5bc181.png) . Тогда она на отрезке
. Тогда она на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png)
Отметьте верные равенства:
Средним значением функции  на отрезке
на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) называется число
называется число
Пусть функция  имеет первообразную на отрезке
имеет первообразную на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) . Тогда она на этом отрезке
. Тогда она на этом отрезке
Не вычисляя интеграла, определить, какие из них имеют знак минус:
Какой должна быть функция сравнения 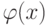 при исследовании на сходимость интеграла
при исследовании на сходимость интеграла 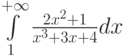 :
:
Рассмотрим несобственные интегралы 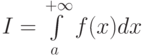 и
и 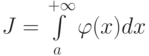 для функций, связанных неравенством
для функций, связанных неравенством 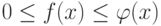 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Рассмотрим несобственный интеграл 1 рода 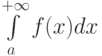 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Рассмотрим несобственные интегралы 2 рода 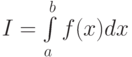 и
и  от неотрицательных на
от неотрицательных на 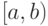 функций, для которых существует конечный предел
функций, для которых существует конечный предел 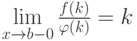 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Пусть 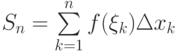 - интегральная сумма функции
- интегральная сумма функции  на
на ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) . Тогда
. Тогда
Число 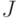 не является пределом интегральных сумм
не является пределом интегральных сумм  функции
функции  на
на ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) , если
, если
Пусть 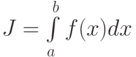 - определённый интеграл функции
- определённый интеграл функции  на
на ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) . Тогда
. Тогда
Пусть 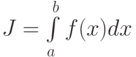 - определённый интеграл функции
- определённый интеграл функции  на
на ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) . Тогда
. Тогда
Отметьте классы интегрируемых на ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) функций:
функций:
Пусть задана функция 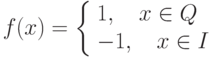 . Тогда на отрезке
. Тогда на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png)
Отметьте верные равенства:
В каких случаях сумма двух функций  может быть интегрируемая:
может быть интегрируемая:
Пусть  и
и  . Отметьте интегрируемые функции на отрезке
. Отметьте интегрируемые функции на отрезке ![[0,1]](https://intuit.ru//sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) :
:
Пусть 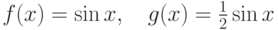 . Для каких отрезков
. Для каких отрезков 
Теорема о среднем справедлива, если функция  :
:
Не вычисляя интегралов, выяснить, для каких функций 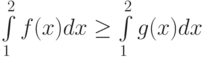 :
:
Пусть 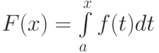 . Тогда эта функция
. Тогда эта функция
Пусть  . Тогда эта функция
. Тогда эта функция
Пусть функция  непрерывна на отрезке
непрерывна на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) . Тогда её первообразная на этом отрезке равна
. Тогда её первообразная на этом отрезке равна
При вычислении каких интегралов применима формула Ньютона-Лейбница:
Какой новый отрезок интегрирования ![[\alpha,\beta]](https://intuit.ru//sites/default/files/tex_cache/76ec9b92b11ea1475095ec6a47fccd53.png) можно взять для вычисления интеграла
можно взять для вычисления интеграла 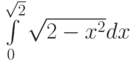 с помощью замены
с помощью замены  :
:
Отметьте условия, при которых справедлива формула интегрирования по частям 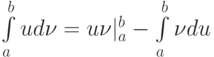 :
:
Площадь криволинейной трапеции для непрерывной и отрицательной функции  на
на ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) равна
равна
Площадь фигуры, ограниченной линиями 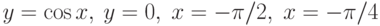 вычисляется по формуле
вычисляется по формуле
Пусть площадь криволинейной трапеции, заданной параметрически 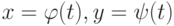 , вычисляется по формуле
, вычисляется по формуле 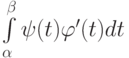 . Тогда на отрезке
. Тогда на отрезке  должны выполняться условия:
должны выполняться условия:
Объём какого тела можно вычислить:
Объем тела с известными поперечными сечениями 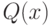 вычисляется по формуле
вычисляется по формуле  . Тогда
. Тогда
Площадь поперечного сечения тела вращения равна:
Длина 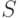 кривой
кривой 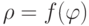 в полярных координатах вычисляется по формуле
в полярных координатах вычисляется по формуле
При вычислении длины кривой в прямоугольных координатах функция 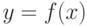 на отрезке
на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) должна удовлетворять условиям:
должна удовлетворять условиям:
Длина кардиоиды  вычисляется по формуле :
вычисляется по формуле :
Работа переменной  силы на отрезке
силы на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) вычисляется по формуле
вычисляется по формуле
Отметьте верные утверждения:
Рассмотрим интеграл 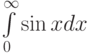 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Отметьте верные утверждения:
Рассмотрим несобственные интегралы 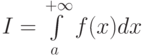 и
и 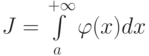 от неотрицательных функций, для которых существует конечный предел
от неотрицательных функций, для которых существует конечный предел 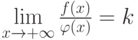 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Интеграл 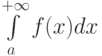 называется абсолютно сходящимся, если
называется абсолютно сходящимся, если
Отметьте верные утверждения:
Пусть задан интеграл 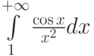 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Пусть задан интеграл  . Отметьте верные утверждения:
. Отметьте верные утверждения:
Рассмотрим несобственные интегралы 2 рода 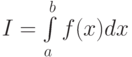 и
и  для функций, связанных неравенством
для функций, связанных неравенством 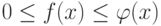 на
на 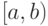 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Пусть задан интеграл  . Отметьте верные утверждения:
. Отметьте верные утверждения:
Функция  - интегрируема по Риману на
- интегрируема по Риману на ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) . Тогда функция
. Тогда функция  на
на ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) всегда
всегда
Пусть площадь криволинейной трапеции, заданной параметрически 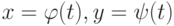 , вычисляется по формуле
, вычисляется по формуле 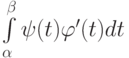 . Тогда на отрезке
. Тогда на отрезке  должны выполняться условия:
должны выполняться условия:
Отметьте условия, при которых справедлива формула интегрирования по частям 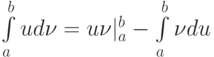 :
:
Какую функцию сравнения 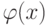 можно рассмотреть для доказательства абсолютной сходимости интеграла
можно рассмотреть для доказательства абсолютной сходимости интеграла 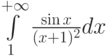 :
:
Какой должна быть функция сравнения 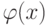 при исследовании на сходимость интеграла
при исследовании на сходимость интеграла 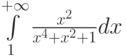 :
:
Отметьте верные утверждения:
Пусть задан интеграл 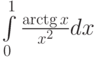 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Пусть задана функция  . Тогда она на отрезке
. Тогда она на отрезке ![[0,1]](https://intuit.ru//sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png)
В каких случаях сумма двух функций  всегда не интегрируемая:
всегда не интегрируемая:
Пусть 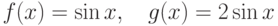 . Для каких отрезков
. Для каких отрезков 
Пусть задана функция 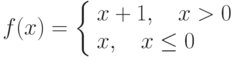 . Тогда эта функция на отрезке
. Тогда эта функция на отрезке ![[-1,1]](https://intuit.ru//sites/default/files/tex_cache/d060b17b29e0dae91a1cac23ea62281a.png)
Найдите производные 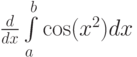 ,
, 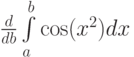 ,
, 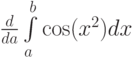 , соответственно:
, соответственно:
Какая формула при выполнении необходимых условий для функций 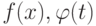 (непрерывности, дифференцируемости, значений на концах отрезка и др.) справедлива:
(непрерывности, дифференцируемости, значений на концах отрезка и др.) справедлива:
На каком отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) для вычисления интеграла
для вычисления интеграла 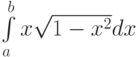 можно применить подстановку
можно применить подстановку  :
:
Площадь фигуры, ограниченной линиями 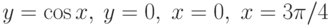 вычисляется по формуле
вычисляется по формуле
Площадь фигуры, ограниченной кривыми  , вычисляется по формуле
, вычисляется по формуле
При вычислении длины кривой, заданной параметрически, функции 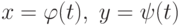 на отрезке
на отрезке ![[t_0,T]](https://intuit.ru//sites/default/files/tex_cache/71e0859cd3bff90002eb796d8f2918a0.png) должны удовлетворять условиям:
должны удовлетворять условиям:
Для несобственного интеграла 1 рода 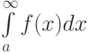 функция
функция  :
:
Рассмотрим интеграл 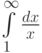 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Рассмотрим несобственные интегралы 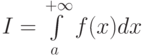 и
и 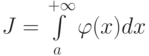 для функций, связанных неравенством
для функций, связанных неравенством 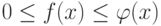 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Рассмотрим несобственный интеграл 1 рода 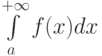 от неотрицательной функции. Отметьте верные утверждения:
от неотрицательной функции. Отметьте верные утверждения:
Какую функцию сравнения 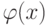 можно рассмотреть для доказательства абсолютной сходимости интеграла
можно рассмотреть для доказательства абсолютной сходимости интеграла  :
:
Несобственный интеграл 2 рода сходится, если предел функции 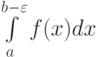 при
при 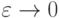
Рассмотрим несобственный интеграл 2 рода 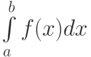 . Отметьте верные утверждения:
. Отметьте верные утверждения:
В каких случаях сумма двух функций  всегда интегрируемая:
всегда интегрируемая:
Пусть задан интеграл 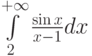 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Площадь криволинейной трапеции для непрерывной и неотрицательной функции  на
на ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) равна
равна
Длина кривой в полярных координатах вычисляется по формуле  . Отметьте верные утверждения:
. Отметьте верные утверждения:
Отметьте условия, при которых справедлива формула замены переменных 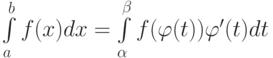
Длина 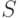 кривой
кривой 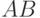
Интеграл 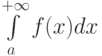 условно сходится. Отметьте верные утверждения:
условно сходится. Отметьте верные утверждения:
Производная интеграла с переменным верхним пределом равна подынтегральной функции в
Объем тела с известными поперечными сечениями 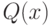 вычисляется по формуле
вычисляется по формуле  . Тогда
. Тогда
Длина окружности на отрезке вычисляется по формуле:
Координата центра тяжести неоднородного стержня плотности 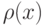 на отрезке
на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) вычисляется по формуле
вычисляется по формуле
Какой должна быть функция сравнения 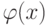 при исследовании на сходимость интеграла
при исследовании на сходимость интеграла  :
:
Рассмотрим несобственные интегралы 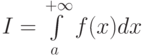 и
и 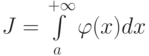 от неотрицательных функций, для которых существует конечный предел
от неотрицательных функций, для которых существует конечный предел 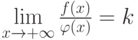 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Рассмотрим несобственные интегралы 2 рода 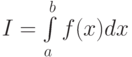 и
и  от неотрицательных на
от неотрицательных на 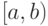 функций, для которых существует конечный предел
функций, для которых существует конечный предел 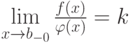 . Отметьте верные утверждения:
. Отметьте верные утверждения:
В каких случаях разность двух функций  всегда не интегрируемая:
всегда не интегрируемая:
Рассмотрим интеграл 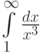 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Пусть 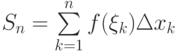 - интегральная сумма функции
- интегральная сумма функции  на
на ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) . Тогда
. Тогда
Какую подстановку можно использовать при вычислении интеграла  :
:
Пусть  - работа переменной
- работа переменной  силы при перемещении материальной точки по прямой из точки
силы при перемещении материальной точки по прямой из точки  в точку
в точку  . Тогда она равна
. Тогда она равна
Координата центра тяжести неоднородного стержня плотности 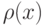 на отрезке
на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) равна
равна 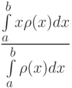 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Пусть интеграл 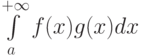 сходится. Отметьте верные утверждения:
сходится. Отметьте верные утверждения:
Площадь криволинейного сектора 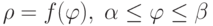 вычисляется по формуле
вычисляется по формуле 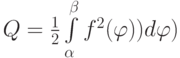 . Тогда
. Тогда
Пусть задана функция 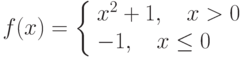 . Тогда эта функция на отрезке
. Тогда эта функция на отрезке ![[-1,1]](https://intuit.ru//sites/default/files/tex_cache/d060b17b29e0dae91a1cac23ea62281a.png)
Дифференциал  длины дуги кривой
длины дуги кривой 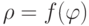 вычисляется по формуле
вычисляется по формуле
Несобственный интеграл 1 рода сходится, если предел функции 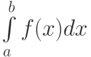 при
при 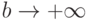
Рассмотрим несобственные интегралы 2 рода 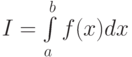 и
и  для функций, связанных неравенством
для функций, связанных неравенством 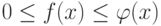 на
на 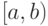 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Пусть задана функция Дирихле 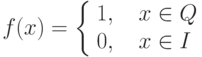 . Тогда она на отрезке
. Тогда она на отрезке ![[0,1]](https://intuit.ru//sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png)
Отметьте условия, при которых справедлива формула замены переменных 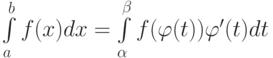
Дифференциал  длины дуги кривой
длины дуги кривой 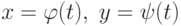 вычисляется по формуле
вычисляется по формуле

 вычисляется по формуле
вычисляется по формуле ![\int\limits_a^b[f(x)-g(x)]dx](https://intuit.ru//sites/default/files/tex_cache/57673ffb275d75cc9b911691b8b77aa5.png) . Какие условия должны выполняться:
. Какие условия должны выполняться: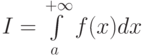 и
и 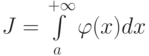 для функций, связанных неравенством
для функций, связанных неравенством 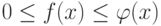 . Отметьте верные утверждения:
. Отметьте верные утверждения: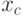 - координата центра тяжести неоднородного стержня плотности
- координата центра тяжести неоднородного стержня плотности 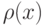 на отрезке
на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) . Тогда она равна отношению к массе стержня
. Тогда она равна отношению к массе стержня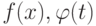 (непрерывности, дифференцируемости, значений на концах отрезка и др.) справедлива:
(непрерывности, дифференцируемости, значений на концах отрезка и др.) справедлива: вычисляется по формуле
вычисляется по формуле ![\int\limits_a^b[f(x)-g(x)]dx](https://intuit.ru//sites/default/files/tex_cache/57673ffb275d75cc9b911691b8b77aa5.png) . Какие условия должны выполняться:
. Какие условия должны выполняться: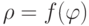 на отрезке
на отрезке ![[\alpha,\beta]](https://intuit.ru//sites/default/files/tex_cache/76ec9b92b11ea1475095ec6a47fccd53.png) должна удовлетворять условиям:
должна удовлетворять условиям: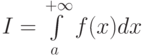 и
и 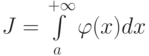 от неотрицательных функций, для которых существует конечный предел
от неотрицательных функций, для которых существует конечный предел 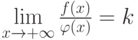 . Отметьте верные утверждения:
. Отметьте верные утверждения: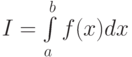 и
и  для функций, связанных неравенством
для функций, связанных неравенством 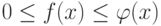 на
на 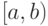 . Отметьте верные утверждения:
. Отметьте верные утверждения: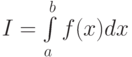 и
и  от неотрицательных на
от неотрицательных на 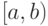 функций, для которых существует конечный предел
функций, для которых существует конечный предел 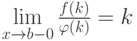 . Отметьте верные утверждения:
. Отметьте верные утверждения: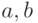 - корни уравнения
- корни уравнения  и
и 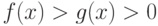 для любого
для любого 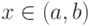 . Тогда площадь фигуры между этими кривыми вычисляется по формуле:
. Тогда площадь фигуры между этими кривыми вычисляется по формуле: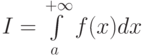 и
и 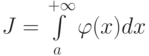 для функций, связанных неравенством
для функций, связанных неравенством 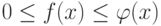 . Отметьте верные утверждения:
. Отметьте верные утверждения: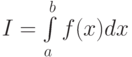 и
и  от неотрицательных на
от неотрицательных на 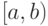 функций, для которых существует конечный предел
функций, для которых существует конечный предел 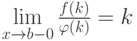 . Отметьте верные утверждения:
. Отметьте верные утверждения: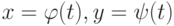 , вычисляется по формуле
, вычисляется по формуле 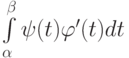 . Тогда на отрезке
. Тогда на отрезке  должны выполняться условия:
должны выполняться условия: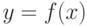 на отрезке
на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) должна удовлетворять условиям:
должна удовлетворять условиям: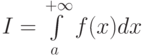 и
и 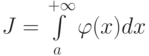 от неотрицательных функций, для которых существует конечный предел
от неотрицательных функций, для которых существует конечный предел 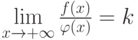 . Отметьте верные утверждения:
. Отметьте верные утверждения: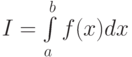 и
и  для функций, связанных неравенством
для функций, связанных неравенством 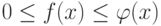 на
на 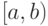 . Отметьте верные утверждения:
. Отметьте верные утверждения: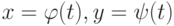 , вычисляется по формуле
, вычисляется по формуле 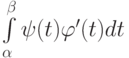 . Тогда на отрезке
. Тогда на отрезке  должны выполняться условия:
должны выполняться условия: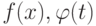 (непрерывности, дифференцируемости, значений на концах отрезка и др.) справедлива:
(непрерывности, дифференцируемости, значений на концах отрезка и др.) справедлива: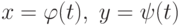 на отрезке
на отрезке ![[t_0,T]](https://intuit.ru//sites/default/files/tex_cache/71e0859cd3bff90002eb796d8f2918a0.png) должны удовлетворять условиям:
должны удовлетворять условиям: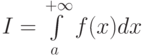 и
и 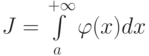 для функций, связанных неравенством
для функций, связанных неравенством 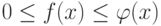 . Отметьте верные утверждения:
. Отметьте верные утверждения: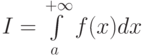 и
и 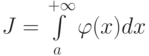 от неотрицательных функций, для которых существует конечный предел
от неотрицательных функций, для которых существует конечный предел 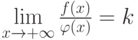 . Отметьте верные утверждения:
. Отметьте верные утверждения: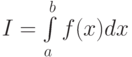 и
и  от неотрицательных на
от неотрицательных на 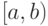 функций, для которых существует конечный предел
функций, для которых существует конечный предел 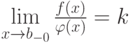 . Отметьте верные утверждения:
. Отметьте верные утверждения: - работа переменной
- работа переменной  силы при перемещении материальной точки по прямой из точки
силы при перемещении материальной точки по прямой из точки  в точку
в точку  . Тогда она равна
. Тогда она равна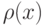 на отрезке
на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) равна
равна 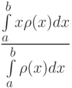 . Отметьте верные утверждения:
. Отметьте верные утверждения: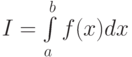 и
и  для функций, связанных неравенством
для функций, связанных неравенством 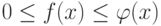 на
на 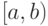 . Отметьте верные утверждения:
. Отметьте верные утверждения: